Ответы
Ответ дал:
0
С учётом ОДЗ (2):
Ответ: x ∈ [-31/8; -15/4)∪ [-2; +∞)
Приложения:
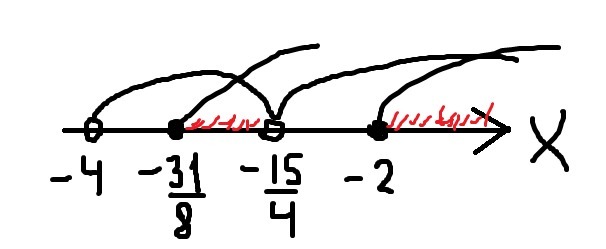
Вас заинтересует
2 года назад
3 года назад
3 года назад
10 лет назад
10 лет назад