Сторона основания правильной треугольной пирамиды равна 3√3, а боковое ребро
наклонено к плоскости основания под углом a, tg a = 5/3. Найти высоту пирамиды.
Варианты ответа
5
5√3
1,8
9√3/5
Ответы
Ответ дал:
0
В треугольнике SHA: ∠H=90°; ; точка H — центр описанной около треугольника АВС окружности, тогда AH — ее радиус.
ед.
Ответ: 5 ед.
Приложения:
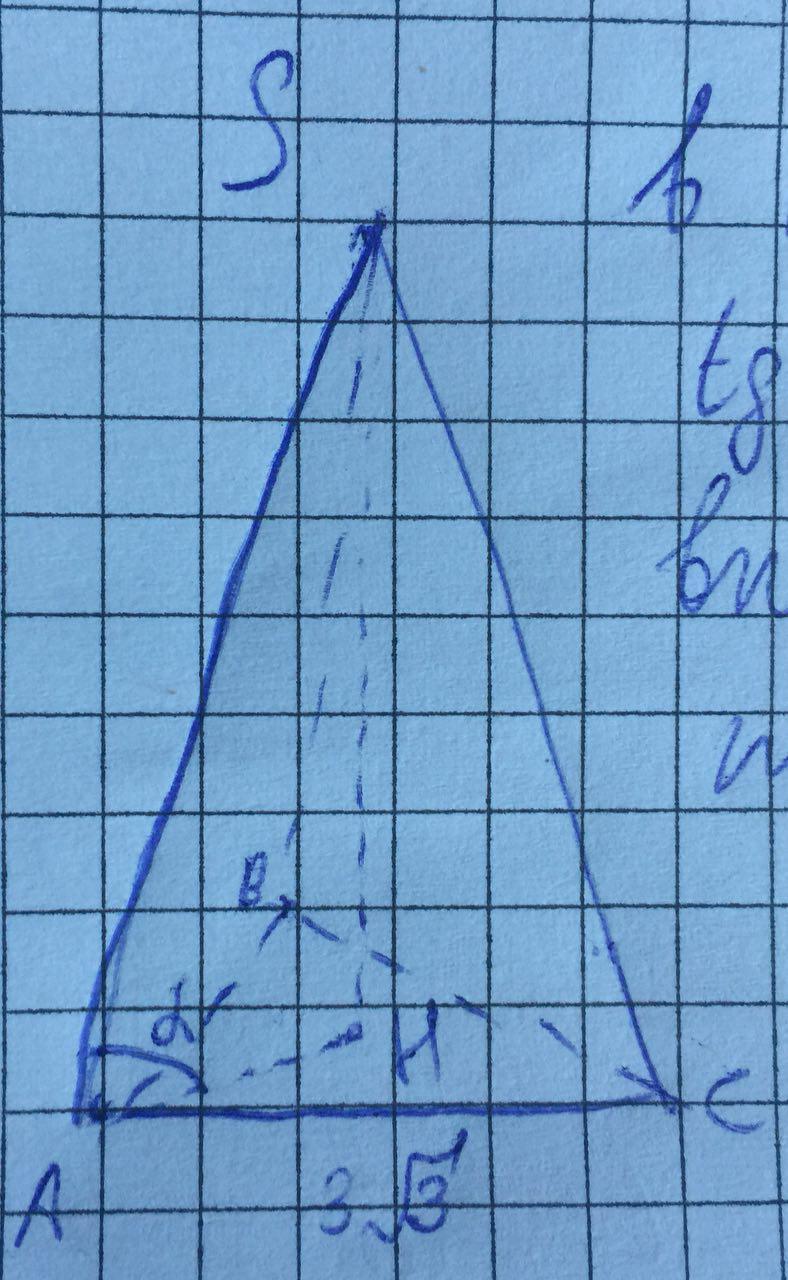
Ответ дал:
0
* Откуда вы взяли √3 в AH = AC / √3?
Ответ дал:
0
кажется, это радиус окружности, вписанной в правильный треугольник
Ответ дал:
0
tg это отношение противолежащего катета к прилежащему, а у вас наоборот?
Ответ дал:
0
точно, ошибся, отметьте нарушение, пожалуйста
Ответ дал:
0
Вы там формулу радиуса описанной окружности используете, а не вписанной?
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад