Ответы
Ответ дал:
0
Ответ:
Приложения:
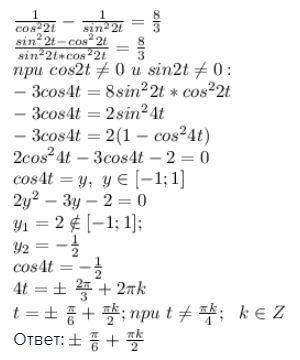
Ответ дал:
0
1/cos²(2t)-1/sin²(2t)=8/3;cos2t≠0;sin2t≠0
sin²2t-cos²2t=8/3*sin²2t*cos²2t
-cos4t=2/3*sin²4t
-3cos4t=2(1-cos²4t)
-3cos4t+2cos²4t-2=0
2cos²4t-3cos4t-2=0
cos4t=a
2a²-3a-2=9
D=9+16=25
a=(3±5)/4
a1=2;a2=-1/2
cos4t=-1/2
4t=±2π/3+2πk
t=±π/6+πk/2;k€Z
sin²2t-cos²2t=8/3*sin²2t*cos²2t
-cos4t=2/3*sin²4t
-3cos4t=2(1-cos²4t)
-3cos4t+2cos²4t-2=0
2cos²4t-3cos4t-2=0
cos4t=a
2a²-3a-2=9
D=9+16=25
a=(3±5)/4
a1=2;a2=-1/2
cos4t=-1/2
4t=±2π/3+2πk
t=±π/6+πk/2;k€Z
Приложения:
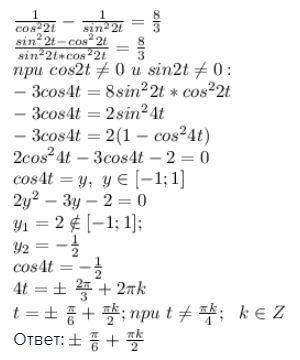
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад