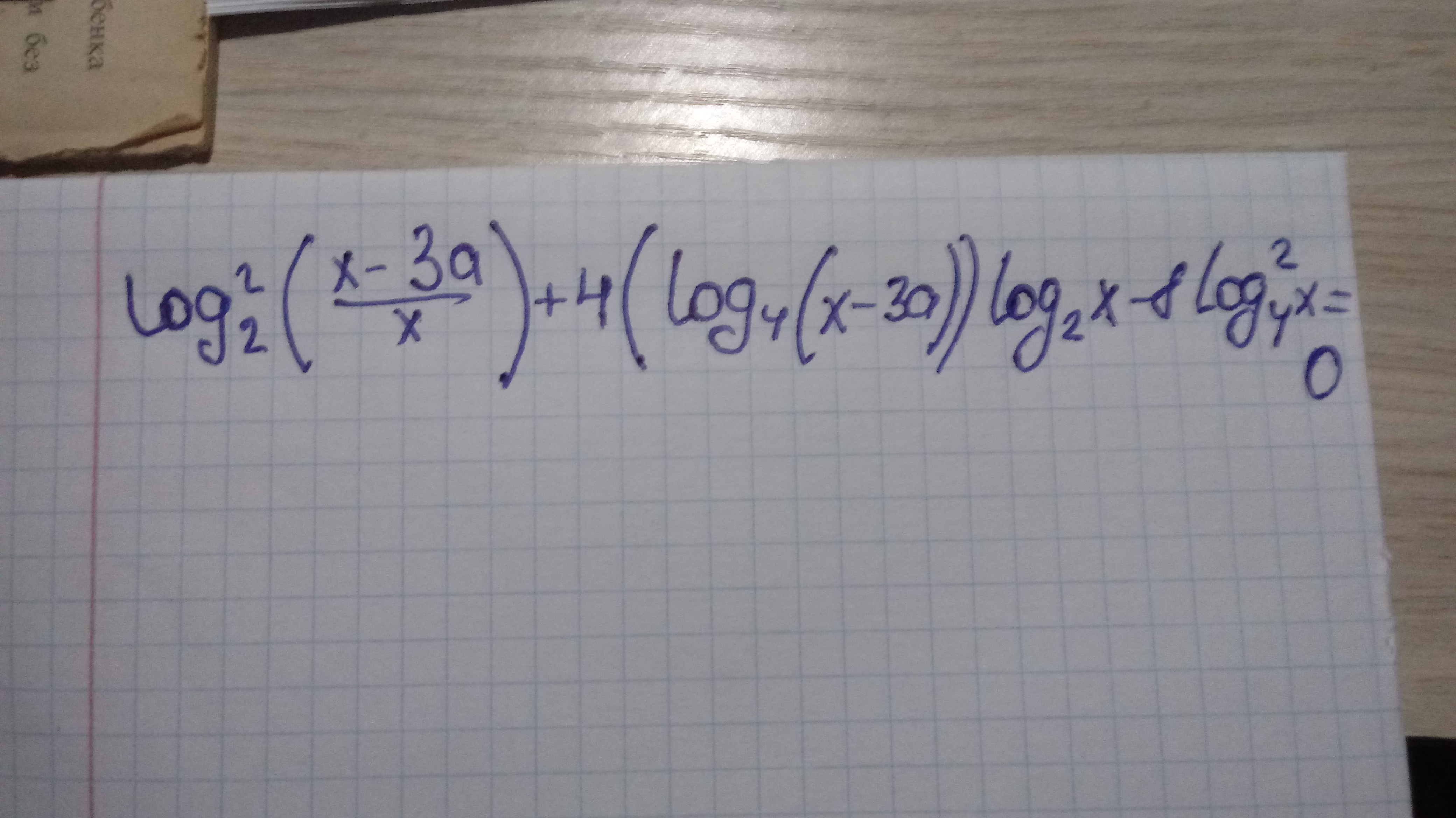Question

Для каждого значения а решить уравнение

Answer 1

ОДЗ: x > 0, x - 3a > 0.

$log_2^2left(dfrac{x-3a}xright)+4log_4(x-3a)log_2x-8log_4^2x=0$

Приводим все логарифмы к одинаковому основанию по формуле $log_{a^k}b=frac1klog_ab$:

$log_2^2left(dfrac{x-3a}xright)+2log_2(x-3a)log_2x-2log_2^2x=0$

Переписываем логарифм частного как разность логарифмов и раскрываем квадрат разности:

$left(log_2(x-3a)-log_2xright)^2+2log_2(x-3a)log_2x-2log_2^2x=0\ (log_2^2(x-3a)-2log_2(x-3a)log_2x+log_2^2x)+\+2log_2(x-3a)log_2x-2log_2^2x=0\ log_2^2(x-3a)-log_2^2x=0$

Получили разность квадратов. Раскладываем на множители:

$(log_2(x-3a)-log_2x)(log_2(x-3a)+log_2x)=0$

Произведение равно нулю, если хотя бы один из сомножителей равен нулю. Значит, уравнение выше на ОДЗ эквивалентно совокупности двух уравнений:

$left[begin{array}{l}log_2(x-3a)-log_2x=0\log_2(x-3a)+log_2x=0end{array}right.quadleft[begin{array}{l}log_2(x-3a)=log_2x\log_2(x-3a)=log_2 dfrac1xend{array}right.\left[begin{array}{l}x-3a=x\x-3a=dfrac1xend{array}right.$

Перед тем, как идти дальше, хочется отметить, что если x > 0, то из равенств выше автоматически x - 3a > 0. Значит, при отборе корней можно будет проверить только неравенство x > 0, второе неравенство из ОДЗ будет выполнено, если выполнено первое.

Решаем дальше:

– первое уравнение совокупности:

x - 3a = x

3a = 0

a = 0

Если a = 0, то решение – x ∈ R (с учетом ограничений ОДЗ x > 0)

– второе уравнение совокупности:

$x-3a=dfrac1x\ x(x-3a)=1\ ((x-1.5a)+1.5a)((x-1.5a)-1.5a)=1\ (x-1.5a)^2-2.25a^2=1\ (x-1.5a)^2=2.25a^2+1>0\ x-1.5a=pmsqrt{2.25a^2+1}\ x=1.5apmsqrt{2.25a^2+1}$

Нужно проверить, при каких a найденное решение удовлетворяет ОДЗ.

1) $x=1.5a+sqrt{2.25a^2+1}>0$

$sqrt{2.25a^2+1}>-1.5a$

Если a > 0, неравенство выполняется: левая часть положительна, правая отрицательная.

Пусть a < 0, тогда обе части неравенства положительны, можно возвести в квадрат

$2.25a^2+1>2.25a^2\ 1>0$

Это неравенство выполнено также при всех a.

2) $x=1.5a-sqrt{2.25a^2+1}$

Аналогично первому корню, можно проверить, что этот корень отрицательный при всех a, и поэтому не удовлетворяет ОДЗ.

Ответ: все x > 0 при a = 0, $x=1.5a+sqrt{2.25a^2+1}$ при a ≠ 0.

Answer 2

Так какие значения а получаются? 1)0 и 2)все кроме 0

Answer 3

У тебя ошибка... Там же 8log^2 х по основанию 4... А значит получится 4log^2 х по основанию 2

Answer 4

Там в квадрате. log(4, x) = 1/2 log(2, x), значит, log(4, x)^2 = 1/4 log(2, x)^2