Ответы
Ответ дал:
0
Используем формулу: синус суммы
sin(a+b) ≡ sin(a)*cos(b) + sin(b)*cos(a).
т.к.
0<a<π/2,
0<b<π/2.
то sin(a), cos(a), sin(b), cos(b) - положительны, кроме того.
sin(a)<1, домножаем это на cos(b)>0,
1) sin(a)*cos(b)<cos(b).
аналогично
sin(b)<1, домножаем на cos(a)>0,
2) sin(b)*cos(a)<cos(a),
складываем 1) и 2)
sin(a)*cos(b)+sin(b)*cos(a) < cos(b)+cos(a),
левая часть последнего тождественно равна sin(a+b), поэтому
sin(a+b) < cos(a)+cos(b).
Ответ дал:
0
Ответ на картинке внизу страницы
Приложения:
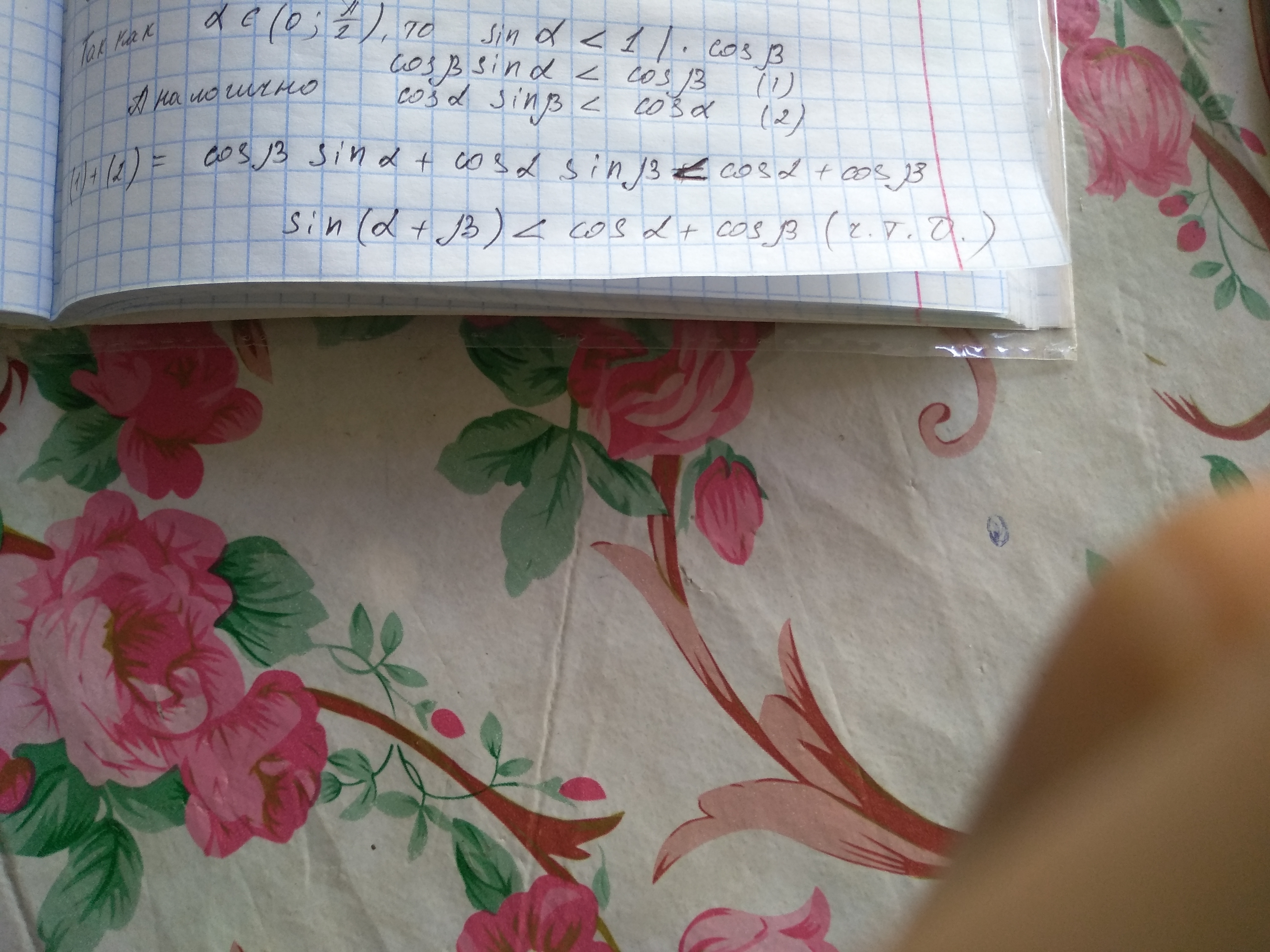
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад