Question

Помогите найти наименьшее целое неравенство. На листочке пожалуйста решение

Answer 1

Решение на фото , удачи

Answer 2

$displaystylemathtt{frac{(x-2)(x+2)(x^2-5x-16)}{(x+2)(x^2-2x+4)}geq0;~left{{{frac{(x-2)(x^2-5x-16)}{x^2-2x+4}geq0}atop{xneq-2}}right}$

окончательно имеем дело с системой $displaystylemathtt{left{{{(x-2)(x^2-5x-16)geq0}atop{xneq-2}}right}$ (домножили неравенство системы на $mathtt{x^2-2x+4=(x-1)^2+3>0}$; также учитываем, что $mathtt{x=-2}$ — корень второй кратности, поэтому при переходе через него на числовой прямой знак неравенства не меняется)

найдём корни квадратного трёхчлена, чтобы разложить всё неравенство на множители:

$mathtt{D=(-5)^2-4*(-16)=89}$, следовательно, $mathtt{x=frac{5бsqrt{89}}{2}}$

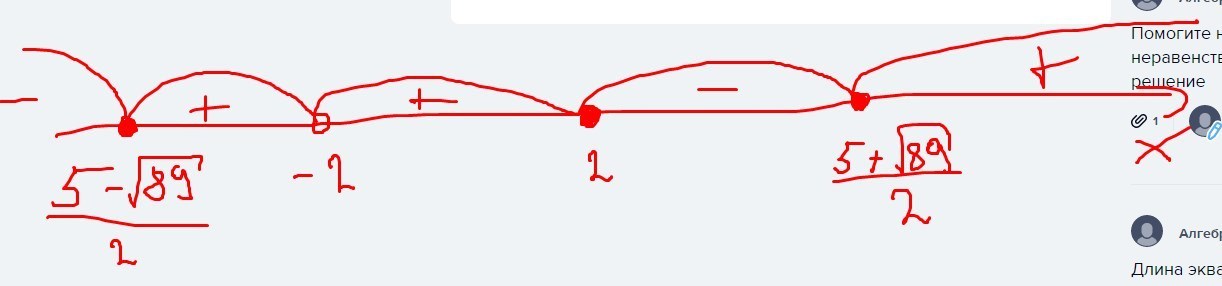
$mathtt{(x-2)(x-frac{5-sqrt{89}}{2})(x-frac{5+sqrt{89}}{2})geq0}$; получается, $mathtt{xin[frac{5-sqrt{89}}{2};-2)U(-2;2]U[frac{5+sqrt{89}}{2};+infty)}$ (решение неравенства методом интервалов в приложении) и, следовательно, наименьшее целое решение равно –1 (решение $mathtt{x=frac{5-sqrt{89}}{2}}$, очевидно, не является целым)

Ответ: –1