Question

на сторонах AB и BC треугольника ADC взяты точки D и E соответственно так, что AD:BD = 1:2 и CE:BE = 2:1. Отрезки AE и CD пересекаются в точке O. Найти площадь треугольника ABC, если площадь треугольника BCO равна 1.

В ответах Sabc = 7/4. Требуется полное решение с понятным объяснением.

Answer 1

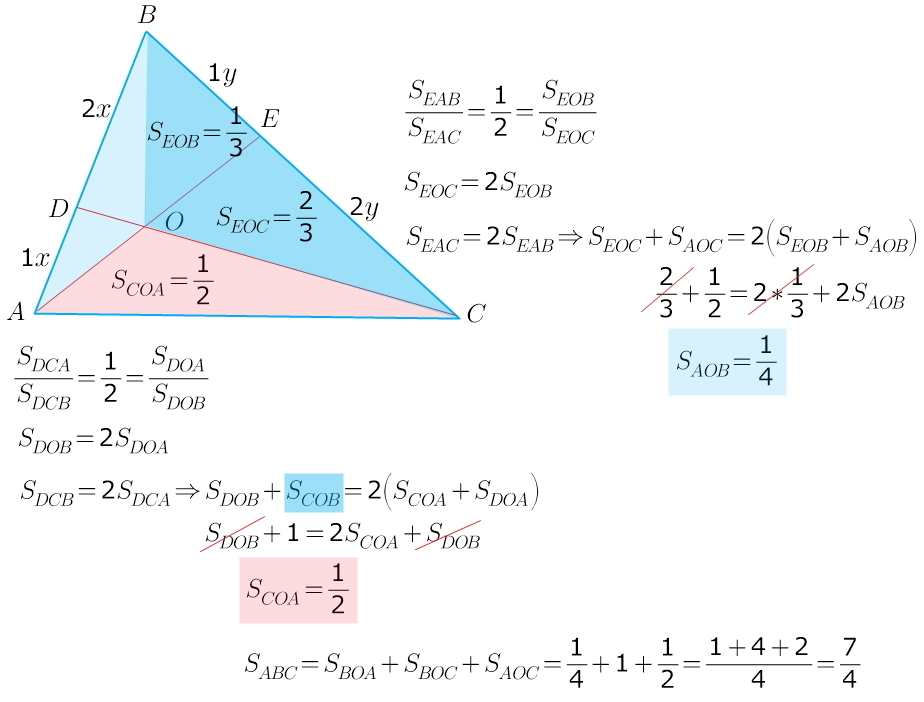
просто аккуратно записать слагаемые для площадей соответствующих треугольников...

Известно: площади треугольников с равными высотами относятся как основания...

например, треугольник ВОА разделен отрезком OD на два треугольника с равными высотами (если провести высоту ОН к основанию АВ)

$frac{S(DOB)}{S(DOA)} =frac{0.5OH*DB}{0.5OH*DA} =frac{DB}{DA} =frac{2}{1}$