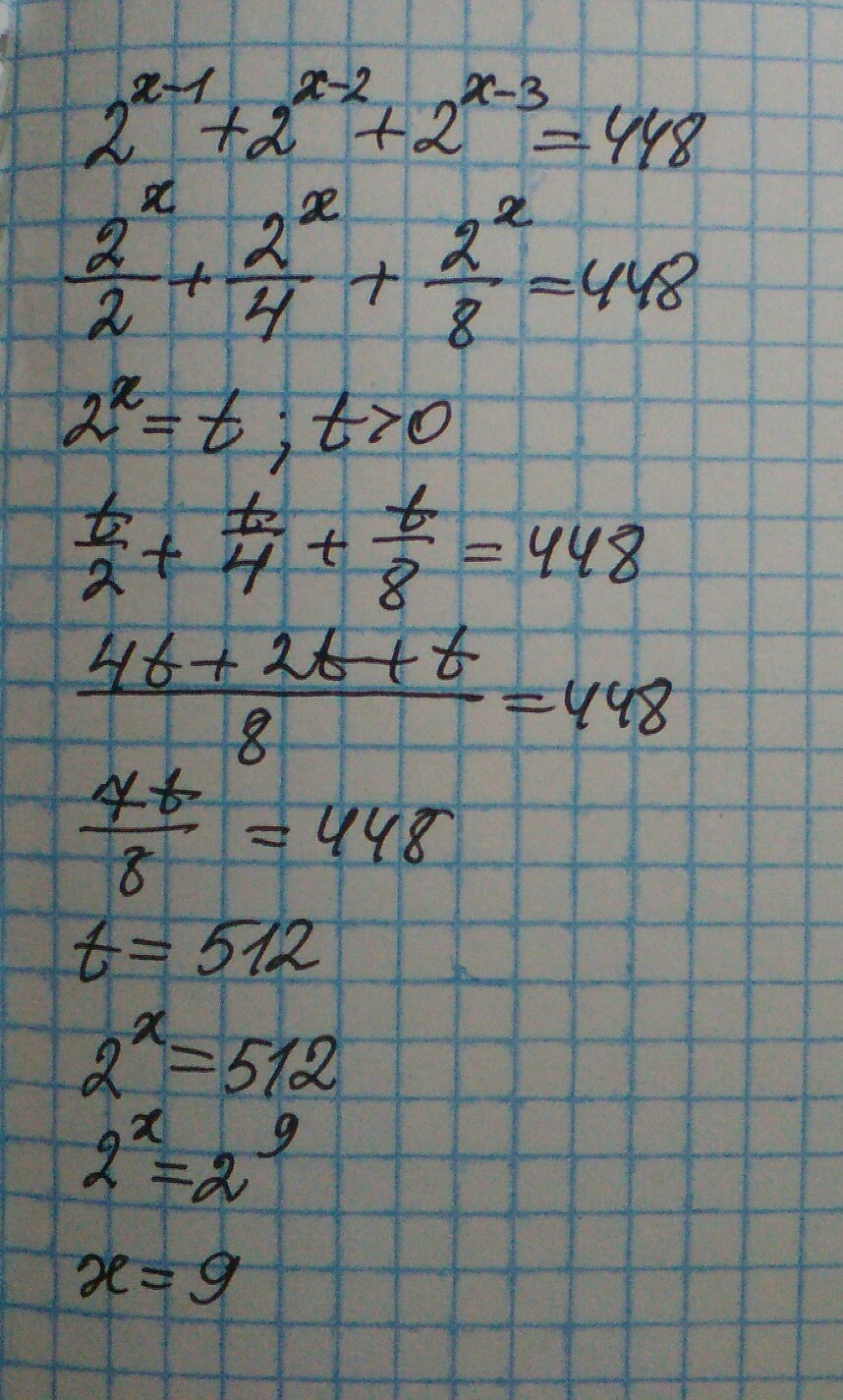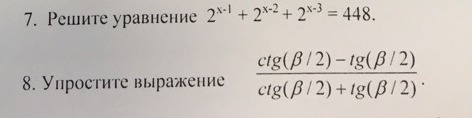Question

Помогите решить, пожалуйста.

Answer 1

Решение во вложениях.

Answer 2

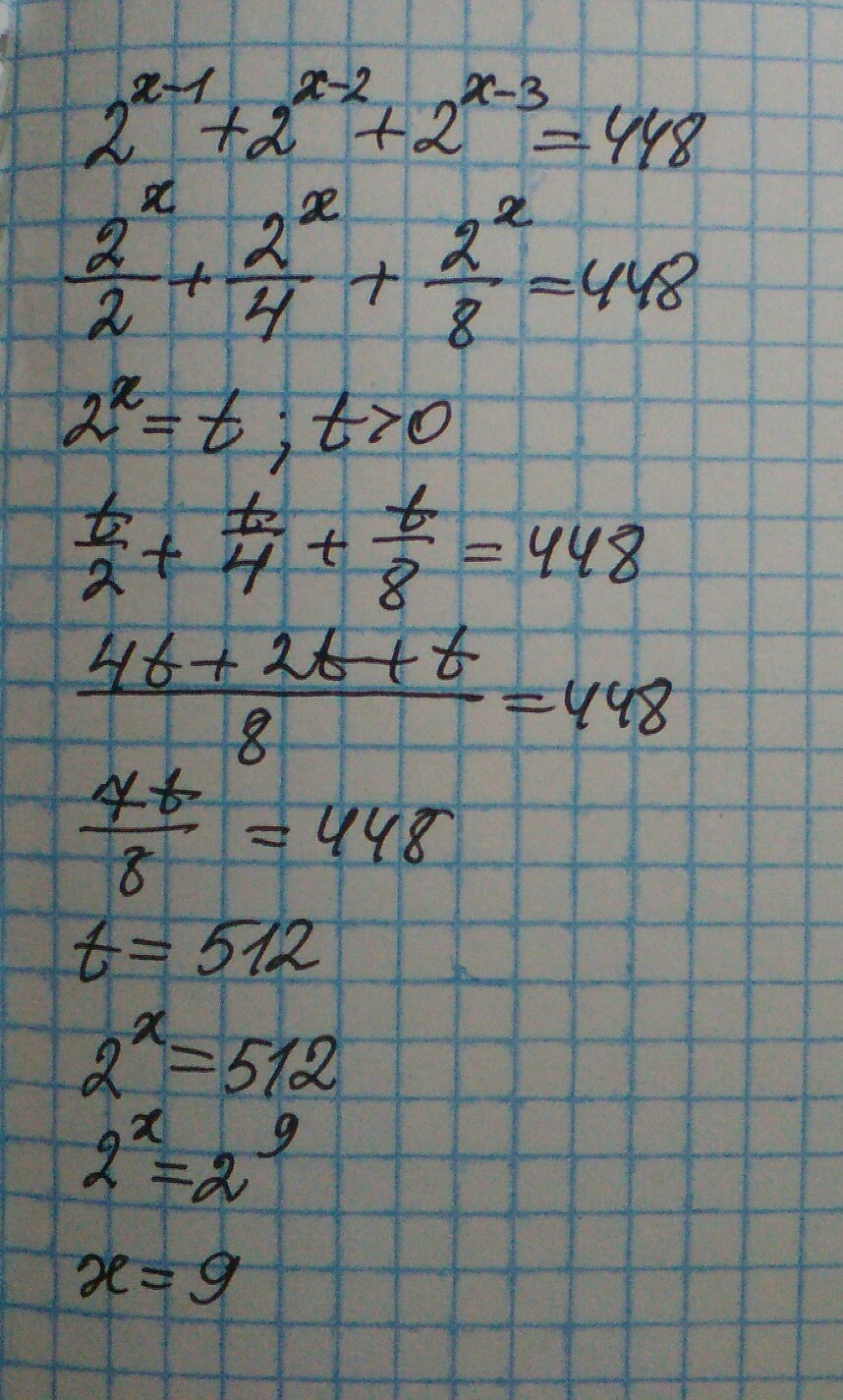
1.

Вынести общий множитель для упрощения вычисления:

(2²+2+1)$2^{x-3}$=448;

Вычислить степень:

(4+2+1)$2^{x-3}$=448;

Вычислить сумму положительных чисел:

7×$2^{x-3}$=448;

Разделить обе стороны уравнения на 7:

2^{x-3} [/tex]=64;

Записать число в виде степени с основанием 2:

2^{x-3} [/tex]=2⁶;

Поскольку основания одинаковы,нужно приравнять показатели:

x-3=6;

Перенести постоянную в правую часть и сменить её знак на противоположный:

x=6+3;

Сложить числа:

x=9

2.

Используя формулу ctg(t)=$frac{1}{tg(t)}$,преобразовать выражение:

$frac{ frac{1}{tg(frac{ beta}{2})}-tg(frac{ beta}{2})}{ frac{1}{tg(frac{ beta}{2})}+tg(frac{ beta}{2})}$;

Записать все числители над общим знаменателем:

$frac{ frac{1-tg(frac{ beta}{2})^{2}}{tg(frac{ beta}{2})}}{frac{1+tg(frac{ beta}{2})^{2}}{tg(frac{ beta}{2})}}$;

Упростить выражение:

$frac{1-tg( frac{ beta}{2})^{2}}{1+tg( frac{ beta}{2})^{2}}$;

Используя формулу tg(t)=$frac{sin(t)}{cos(t)}$,преобразовать выражение:

$frac{1-( frac{sin(frac{beta}{2})}{cos( frac{ beta }{2})})^{2}}{1+(frac{sin(frac{beta}{2})}{cos( frac{ beta }{2})})^{2}}$;

Чтобы возвести дробь в степень,нужно возвести в эту степень числитель и знаменатель:

$frac{1-frac{sin( frac{ beta}{2})^{2}}{cos( frac{ beta}{2})^{2}}}{1+frac{sin( frac{ beta}{2})^{2}}{cos( frac{ beta}{2})^{2}}}$;

Записать все числители над общим знаменателем:

$frac{frac{cos( frac{ beta}{2})^{2}-sin(frac{ beta}{2})^{2}}{cos(frac{ beta}{2})^{2}}}{frac{cos( frac{ beta}{2})^{2}+sin(frac{ beta}{2})^{2}}{cos(frac{ beta}{2})^{2}}}$;

Упростить составную дробь:

$frac{cos(frac{ beta}{2})^{2}-sin(frac{ beta}{2})^{2}}{cos(frac{ beta}{2})^{2}+sin(frac{ beta}{2})^{2}}$;

Упростить выражение,используя формулу cos(t)²-sin(t)²=cos(2t):

$frac{cos(beta)}{1}$;

Любое выражение,разделённое на 1,равно самому себе:

cos(β)