Ответы
Ответ дал:
0
Решение во вложении
Приложения:
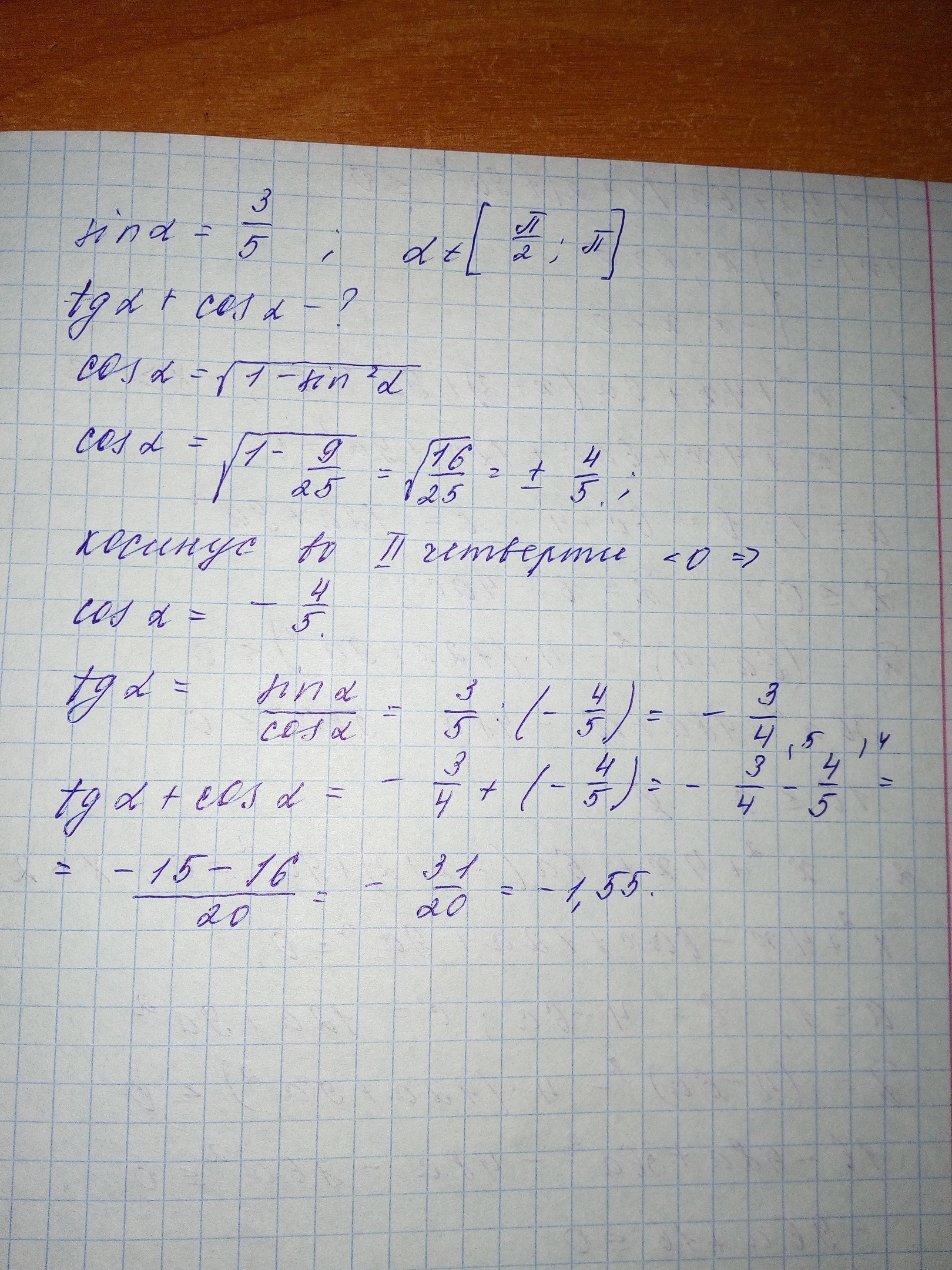
Ответ дал:
0
из основного тригонометрического тождества найдем косинус:



т. к. a Є [90,180], то косинус отрицательный

тангенс - синус делить на косинус

tga+cosa=

т. к. a Є [90,180], то косинус отрицательный
тангенс - синус делить на косинус
tga+cosa=
Приложения:
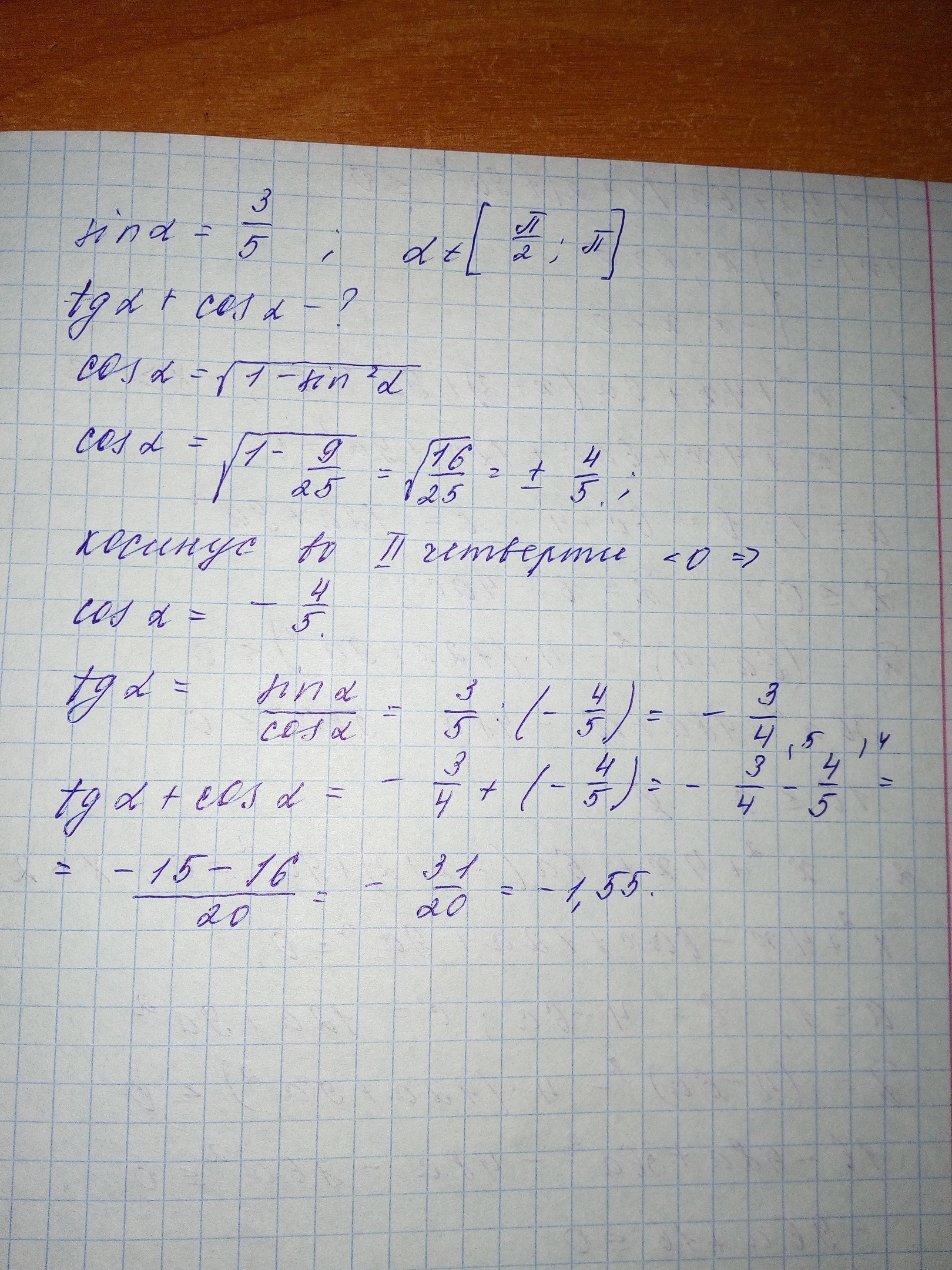
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад