Question

Решите уравнение
5cosx+4 дробь 4tgx-3=0

Answer 1

1) Делаем ОДЗ в фигурных скобках:

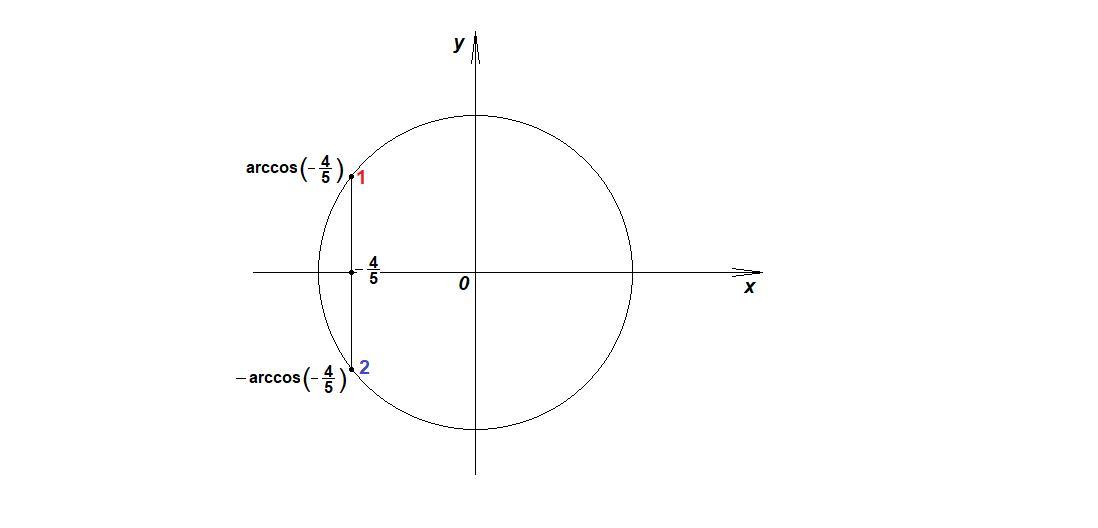
cos x = -4/5 , x принадлежит 2й четверти

tg x НЕ равен 3/4, x принадлежит 3й четверти

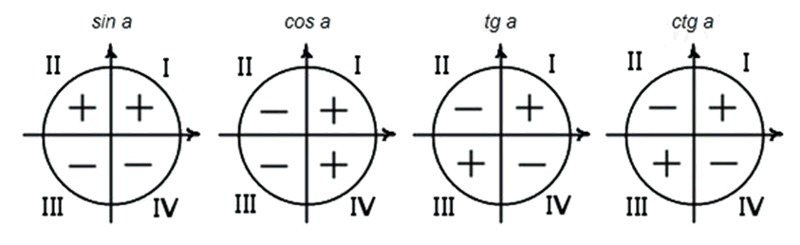
Дело в том, что минус у синуса это вторая и третья четверти(-4/5)

У тангенса положительные четверти 1 и 3. tg x принадлежит 3 четверти, т.к. положительный знак в первой четверти cos и tg совпадает.

Из уравнения cosx = -4/5 получаем:

+- arccos(-4/5) + 2 Пк

то есть

arccos(-4/5) + 2 Пк= П-arccos 4/5 +2 Пк

и

- arccos(-4/5) = -(П-arccos4/5) + 2Пк

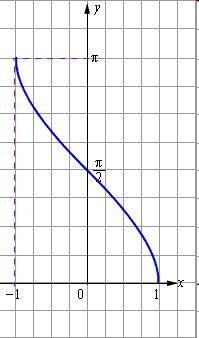
По графику арккосинуса определяем, что arccos 4/5 примерно равно П/3. Значит:

arccos(-4/5) + 2 Пк= П-arccos 4/5 +2 Пк ( примерно: П-п/3 = 2п/3), значит, х прин. 2 четверти консинуса

и

- arccos(-4/5) = -П-arccos4/5 + 2Пк( примерно: -П-п/3 = -(П-п/3) = МИНУС 2п/3, х прин 3 чет косинуса

но х принадлежит 2, а не 3 четверти

значит, х= П-arccos4/5+2Пn, n прин. Z

Answer 2

Дело в том, что минус у КОСИНУСА это вторая и третья четверти(-4/5)...

Answer 3

Ответ:

$x=pi -arccosfrac{4}{5}+2pi n$,   n∈Z

Объяснение:

$dfrac{5cosx+4}{4tgx-3}=0$

Дробь равна нулю, если числитель равен нулю, а знаменатель не равен нулю:

$left { {{5cosx+4=0} atop {4tgx-3neq 0}} right.$

$left { {{cosx=-frac{4}{5}} atop {tgxneq frac{3}{4} }} right.$

Решим первое уравнение:

$cosx=-dfrac{4}{5}$

$x=pm arccos(-frac{4}{5})+2pi n$

Точки, соответствующие корням уравнения, отмечены на числовой окружности.

Найдем значения tgx, если cosx = - 4/5:

$tg^{2}x+1=frac{1}{cos^{2}x}$

$tg^{2}x=frac{25}{16}-1$

$tg^{2}x=frac{9}{16}$

$tgx=frac{3}{4}$     или      $tgx=-frac{3}{4}$

В точке (2) $tgx=frac{3}{4}$ (так как в третьей четверти tgx > 0), а значит знаменатель превращается в нуль, значит корень

$x=-arccos(-frac{4}{5})+2pi n$ не подходит.

В точке (1) $tgx=-frac{3}{4}$   (так как во второй четверти tgx < 0), значит подходит корень

$x=arccos(-frac{4}{5})+2pi n$

$x=(pi -arccosfrac{4}{5})+2pi n$,   n∈Z