Question

Вторая производная функции одной переменной

Answer 1

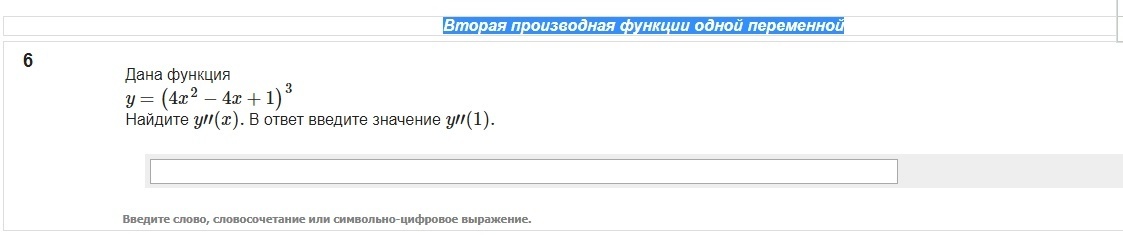
y = (2x - 1)⁶

y' = 12(2x-1)⁵

y'' = 120(2x-1)⁴

y''(1) = 120(2-1)⁴ = 120

Ответ: 120

Answer 2

Да ,я просто решил немного усложнить ,ради интереса

Answer 3

Такой я)))

Answer 4

а я где-то просчиталась)) а зачем зря усложнять...

Answer 5

вот теперь очень красиво получилось))

Answer 6

Разве не красивое у меня решение?))))

Answer 7

$y=(4x^2-4x+1)^3\y'=3(4x^2-4x+1)^2(4x^2-4x+1)'\y'=3(4x^2-4x+1)^2(8x-4)\y'=(24x-12)(16x^4+16x^2+1-32x^3+8x^2-8x) \y'=384x^5+576x^3+24x-768x^4-192x^4-288x^2-12+384x^3+96x\y'=384x^5-960x^4+960x^3-480x^2+120x-12\y''= 1920x^4-3840x^3+2880x^2-960x+120\y''(1)=4920-4800=120$

Второй способ 

$y=(4x^2-4x+1)^3\y'=3(4x^2-4x+1)^2(4x^2-4x+1)'\ y'=3(4x^2-4x+1)^2(8x-4)\y'=(4x^2-4x+1)^2(24x-12)\y''=((4x^2-4x+1)^2)'(24x-12)+(4x^2-4x+1)^2(24x-12)'\y''=2(4x^2-4x+1)(8x-4)(24x-12)+(4x^2-4x+1)^2*24\y''=(24x^2-24x+6)(64x^2-64x+16)+24(4x^2-4x+1)^2\y''(1)=(24-24+6)(64-64+16)+24(4-4+1)^2\y''(1)=6*16+24=120$