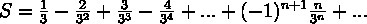Question

Сумма S существует и конечна. Найдите ее.

Answer 1

$sum_{n=0}^infty x^n = frac{1}{1-x}$

для x в промежутке (-1,1), так как при таких х это будет убывающая геометрическая прогрессия.

Продифференциировав такой ряд получим

$( sum_{n=0}^infty x^n)' = sum_{n=0}^infty (x^n)' = sum_{n=0}^infty nx^{n-1}= (frac{1}{1-x} )' = frac{1}{(1-x)^2}$

Домножим левую часть на х и 1x, получим

$frac{1}{x} sum_{n=0}^infty nx^n = frac{1}{(1-x)^2} \ \ sum_{n=0}^infty nx^n = frac{x}{(1-x)^2}$

-13 попадает в промежуток (-1,1), так что -13 можно подставить в наше выражение:

$sum_{n=0}^infty n(-frac{1}{3})^n = sum_{n=0}^infty (-1)^nfrac{n}{3^n} = -sum_{n=0}^infty (-1)^{n+1}frac{n}{3^n} = \ \ =-frac{-frac{1}{3}}{(1-(-frac{1}{3}))^2} =-( -frac{1}{3} * frac{9}{16}) = frac{3}{16}$