Предмет: Математика
Автор: sokolin2
Вопрос задан 8 лет назад

Помогите решить!!
Объём шара равен 6. Найдите объём цилинра , ВПИСАННОГО в шар.

Ответы

Ответ дал: mefody66

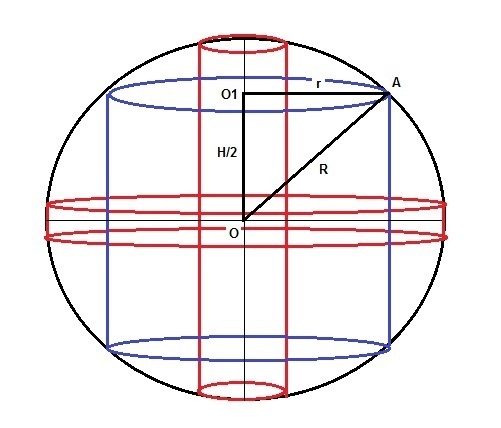
В шар можно вписать много разных цилиндров, несколько из них показано на рисунке. Обозначим r радиус цилиндра, H высоту. R радиус шара.

В крайних положениях, при R = r и при H = 2R будет объем цилиндра V(ц) = 0.

Близкие к этому положения показаны красным.

В некотором положении объем цилиндра будет максимальным.

Это положение показано синим.

Объем шара V(ш) = 4/3*pi*R^3 = 6

R^3 = 6*3/(4pi) = 9/(2pi) = 27/(6pi)

R = ∛(27/(6pi)) = 3/∛(6pi)

По теореме Пифагора (треугольник показан черным)

(H/2)^2 + r^2 = R^2 = 9/∛(36pi^2)

$r^2=frac{9}{sqrt[3]{36pi^2}} -frac{H^2}{4} =sqrt[3]{frac{9^3}{9*4pi^2}} -frac{H^2}{4} =sqrt[3]{frac{81}{4pi^2}}-frac{H^2}{4}$

Объем цилиндра

$V=pi r^2H=pi (sqrt[3]{frac{81}{4pi^2}}-frac{H^2}{4})H=pi Hsqrt[3]{frac{81}{4pi^2}}-frac{pi}{4} H^3=Hsqrt[3]{frac{81pi}{4}}-frac{pi}{4} H^3$

Объем будет максимальным, когда производная будет равна 0

$V'(H)=sqrt[3]{frac{81pi}{4}}-frac{3pi}{4} H^2=0$

$H^2=sqrt[3]{frac{81pi}{4}}:frac{3pi}{4}=sqrt[3]{frac{81pi}{4}*frac{64}{27pi^3}}=sqrt[3]{frac{3*16}{pi^2}}=sqrt[3]{frac{48}{pi^2}}$

$H=sqrt[6]{frac{48}{pi^2}}$

Теперь найдем радиус цилиндра

$r^2=sqrt[3]{frac{81}{4pi^2}}-frac{H^2}{4} =sqrt[3]{frac{81}{4pi^2}}-frac{1}{4}sqrt[3]{frac{48}{pi^2}}=sqrt[3]{frac{81}{4pi^2}}-sqrt[3]{frac{48}{64pi^2}}=$

$=sqrt[3]{frac{81}{4pi^2}}-sqrt[3]{frac{3}{4pi^2}} =frac{sqrt[3]{81}-sqrt[3]{3}}{sqrt[3]{4pi^2}}= frac{3 sqrt[3]{3} - sqrt[3]{3} }{ sqrt[3]{4 pi^2 } } = frac{2 sqrt[3]{3} }{sqrt[3]{4 pi^2 } } = sqrt[3]{ frac{8*3}{4 pi^2 } } = sqrt[3]{ frac{6}{pi^2} }$
Объем цилиндра
$V=pi r^2H=pi sqrt[3]{ frac{6}{ pi ^2} } *sqrt[6]{frac{48}{pi^2}} = sqrt[6]{ frac{36 pi ^6}{ pi ^4} } *sqrt[6]{frac{48}{pi^2}} =sqrt[6]{36*48} = sqrt[6]{6^3*8} =sqrt{12}$

Приложения: