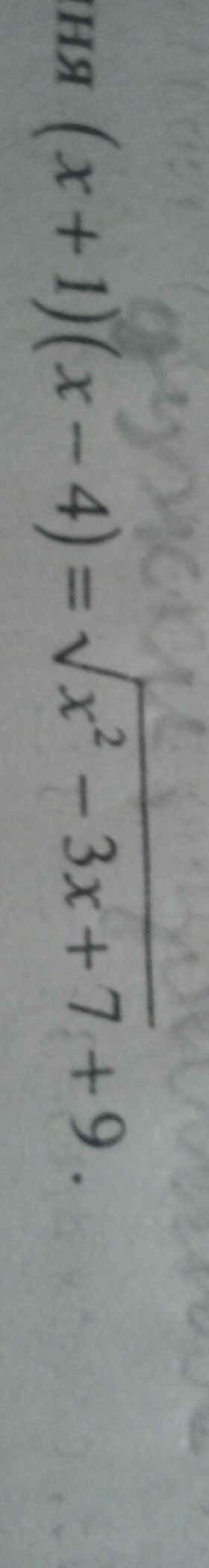Ответы
Ответ дал:
0
Ответ: -3; 6.
Приложения:
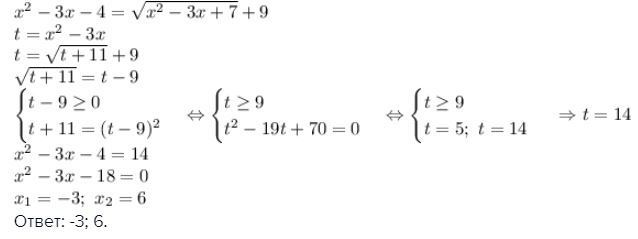
Ответ дал:
0
(x + 1)(x - 4) = √(x² - 3x + 7) + 9
ОДЗ:
(x + 1)(x - 4) ≥ 0
x ∈ (-∞; -1] U [4; +∞)
x² + x - 4x - 4 = √(x² - 3x + 7) + 9
x² - 3x - 13 = √(x² - 3x + 7)
Пусть x² - 3x + 7 = t
Тогда:
t - 20 = √t
t - √t - 20 = 0
D = 1 - 4*(-20) = 81
√t = (1 + 9)/2 = 5
√t = (1 - 9)/2 = -4, не удовл.
t = 25
x² - 3x + 7 = 25
x² - 3x - 18 = 0
D = 9 - 4*(-18) = 81
x1 = (3 + 9)/2 = 6
x2 = (3 - 9)/2 = -3
Проверка:
(6 + 1)(6 - 4) = √(36 - 18 + 7) + 9
14 = √25 + 9
14 = 5 + 9
14 = 14 -- верно => x = 6 является корнем.
(-3 + 1)(-3 - 4) = √(9 + 9 + 7) + 9
-2*(-7) = √25 + 9
14 = 5 + 9
14 = 14 -- верно => x = -3 является корнем.
Ответ: -3; 6.
Приложения:
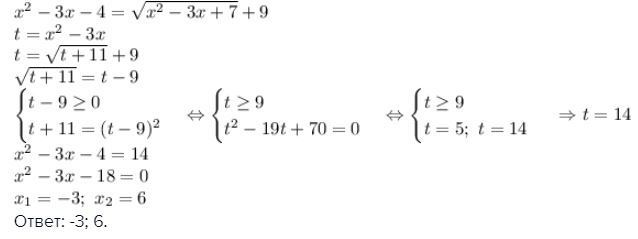
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад