Question

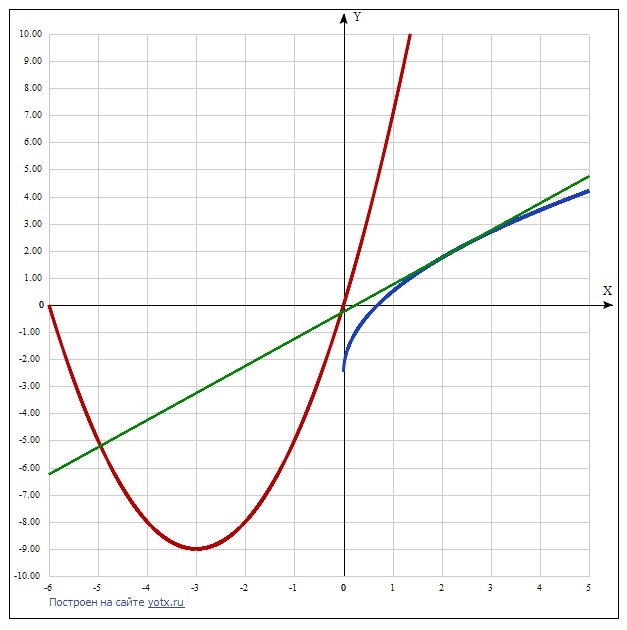
ПОМОГИТЕ ПОЖАЛУЙСТА СРОООЧНО! Найти уравнение прямой которая проходит через точку с координатами (1/4;0), касается графика функции y(x)=3√x-5/2 и пересекает в двух различных точках график функции y(x)=x²+6x

Answer 1

Производная функции у = 3√х-2,5 равна:

y' = 3/(2√x).

Подставляем в уравнение касательной с учётом координат заданной точки:

0 = (3(1 - 4хо) + 6хо - 5√(хо))/(8√хо).

Приравняем нулю числитель с заменой √хо = t.

12t² - 20t + 3 = 0.

Квадратное уравнение, решаем относительно t:

Ищем дискриминант:

D=(-20)^2-4*12*3=400-4*12*3=400-48*3=400-144=256;

Дискриминант больше 0, уравнение имеет 2 корня:

t₁=(√256-(-20))/(2*12)=(16-(-20))/(2*12)=(16+20)/(2*12)=36/(2*12)=36/24=1.5;

t₂=(-√256-(-20))/(2*12)=(-16-(-20))/(2*12)=(-16+20)/(2*12)=4/(2*12)=4/24=1//6≈ 0.16667.

Обратная замена: х₁ = t₁² = 2,25.

x₂ = t₂² = 1/36 этот корень отбрасываем: в этой точке касательная к графику функции не проходит.

Принимаем хо = 2,25, уо = 3*1,5 - 2,5 = 2.

Теперь по координатам двух точек находим уравнение касательной.

(х -(1/2))/2 = у/2.

Ответ: у = х - (1/4).