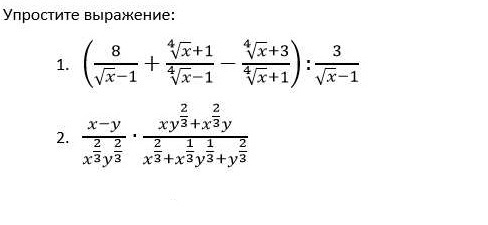Ответы
Ответ дал:
0
1.
![( frac{8}{ sqrt{x} - 1 } + frac{ sqrt[4]{x} + 1}{ sqrt[4]{x} - 1} - frac{ sqrt[4]{x} + 3}{ sqrt[4]{x} + 1} ) div frac{3}{ sqrt{x} - 1} = ( frac{8}{( sqrt[4]{x} - 1)( sqrt[4]{x} + 1) } + frac{ {( sqrt[4]{x} + 1)}^{2} }{( sqrt[4]{x} - 1)( sqrt[4]{x} + 1)} - frac{( sqrt[4]{x} + 3)( sqrt[4]{x} - 1) }{ (sqrt[4]{x} - 1)( sqrt[4]{x} + 1)} div frac{3}{ sqrt{x} - 1} = ( frac{8 + sqrt{x} + 2 sqrt[4]{x} + 1 - sqrt{x} - 3 sqrt[4]{x} + sqrt[4]{x} + 3}{( sqrt[4]{x} - 1)( sqrt[4]{x} + 1) } ) times frac{ sqrt{x} - 1}{3} = frac{12}{ sqrt{x} - 1} times frac{ sqrt{x} - 1}{3} = 4 ( frac{8}{ sqrt{x} - 1 } + frac{ sqrt[4]{x} + 1}{ sqrt[4]{x} - 1} - frac{ sqrt[4]{x} + 3}{ sqrt[4]{x} + 1} ) div frac{3}{ sqrt{x} - 1} = ( frac{8}{( sqrt[4]{x} - 1)( sqrt[4]{x} + 1) } + frac{ {( sqrt[4]{x} + 1)}^{2} }{( sqrt[4]{x} - 1)( sqrt[4]{x} + 1)} - frac{( sqrt[4]{x} + 3)( sqrt[4]{x} - 1) }{ (sqrt[4]{x} - 1)( sqrt[4]{x} + 1)} div frac{3}{ sqrt{x} - 1} = ( frac{8 + sqrt{x} + 2 sqrt[4]{x} + 1 - sqrt{x} - 3 sqrt[4]{x} + sqrt[4]{x} + 3}{( sqrt[4]{x} - 1)( sqrt[4]{x} + 1) } ) times frac{ sqrt{x} - 1}{3} = frac{12}{ sqrt{x} - 1} times frac{ sqrt{x} - 1}{3} = 4](https://tex.z-dn.net/?f=%28+frac%7B8%7D%7B+sqrt%7Bx%7D+-+1+%7D++%2B++frac%7B+sqrt%5B4%5D%7Bx%7D++%2B+1%7D%7B+sqrt%5B4%5D%7Bx%7D++-+1%7D++-++frac%7B+sqrt%5B4%5D%7Bx%7D++%2B+3%7D%7B+sqrt%5B4%5D%7Bx%7D++%2B+1%7D+%29+div++frac%7B3%7D%7B+sqrt%7Bx%7D++-+1%7D++%3D+%28+frac%7B8%7D%7B%28++sqrt%5B4%5D%7Bx%7D+++-+1%29%28+sqrt%5B4%5D%7Bx%7D+%2B+1%29+%7D++%2B++frac%7B+%7B%28+sqrt%5B4%5D%7Bx%7D++%2B+1%29%7D%5E%7B2%7D+%7D%7B%28+sqrt%5B4%5D%7Bx%7D++-+1%29%28+sqrt%5B4%5D%7Bx%7D++%2B+1%29%7D+++-++frac%7B%28+sqrt%5B4%5D%7Bx%7D+%2B+3%29%28+sqrt%5B4%5D%7Bx%7D++-+1%29+%7D%7B+%28sqrt%5B4%5D%7Bx%7D++-+1%29%28+sqrt%5B4%5D%7Bx%7D++%2B+1%29%7D+++div++frac%7B3%7D%7B+sqrt%7Bx%7D++-+1%7D++%3D+%28+frac%7B8+%2B++sqrt%7Bx%7D+%2B+2+sqrt%5B4%5D%7Bx%7D+++%2B+1+-++sqrt%7Bx%7D+-+3+sqrt%5B4%5D%7Bx%7D+++%2B++sqrt%5B4%5D%7Bx%7D++%2B+3%7D%7B%28+sqrt%5B4%5D%7Bx%7D+-+1%29%28+sqrt%5B4%5D%7Bx%7D++%2B+1%29+%7D++%29+times++frac%7B+sqrt%7Bx%7D++-+1%7D%7B3%7D++%3D++frac%7B12%7D%7B+sqrt%7Bx%7D++-+1%7D++times++frac%7B+sqrt%7Bx%7D++-+1%7D%7B3%7D++%3D+4)
2.

2.
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад