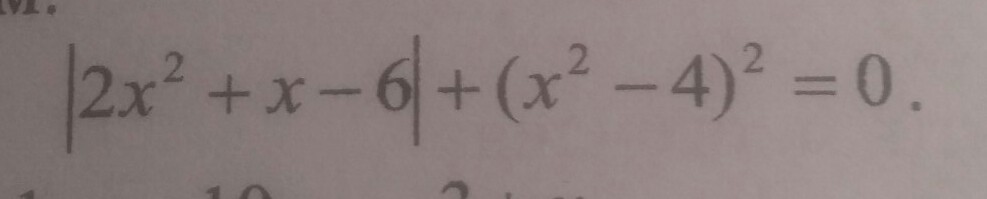Ответы
Ответ дал:
0
Так как |2x²+x-6|≥0 при любом x и (x²-4)²≥0 при любом x, то равенство верно только при
Ответ: x=-2
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
10 лет назад