Дам 25 баллов!
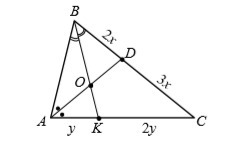
В треугольнике ABC биссектриса AD делит сторону BC в отношении BD:DC=2:3, а биссектриса BK делит сторону AC в отношении AK:KC=1:2. Чему равно отношение длин сторон треугольника ? ABC В каком отношении биссектриса BK разделила биссектрису AD, т. е. чему равно AO:OD?
Приложения:
Ответы
Ответ дал:
0
обозначим для краткости АB = a
по условию: BC = 5x; AC = 3y
известно: биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам.
2x / a = 3x / 3y ---> a = 2y ( y = 0.5a )
2y / 5x = y / a ---> 2a = 5x ---> a = 2.5x ( x = 0.4a )
отношение длин сторон:
AB : BC = a / 5x = 2.5x / 5x = 1 : 2
AB : AC = a / 3y = 2y / 3y = 2 : 3
BC : AC = 5x / 3y = (5*0.4a) : (3*0.5a) = 2 : 1.5 = 4 : 3
AO : OD = AB : BD ---> AO : OD = 2.5x : 2x = 5 : 4
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад
10 лет назад