Question

Надо найти точку, в которой функция принимает наименьшее значение на отрезке [10;12]

Answer 1

y=log₂(x²-16x+80)

Найдем первую производную и приравняем к 0, чтобы найти точки max и min:

y'=(log₂(x²-16x+80))'=

=(2x-16)/(ln2•(x²-16x+80))=0

Тогда 2x-16=0 <=> x=8

Находим вторую производную:

y''=(-2x²+32x-96)/(ln2•(x²-16x+80)²)=

=(-2•8²+32•8-96)/(ln2•(8²-16•8+80)²)=

=1/(8ln2)>0, значит x=8 - точка min.

Значит на промежутке [10;12] функция будет возрастать, а следовательно наименьшее значение функция будет иметь в точке x=10, тогда:

y=log₂(x²-16x+80)=

=log₂(10²-16•10+80)=2+log₂5

Ответ: (10;2+log₂5).

Answer 2

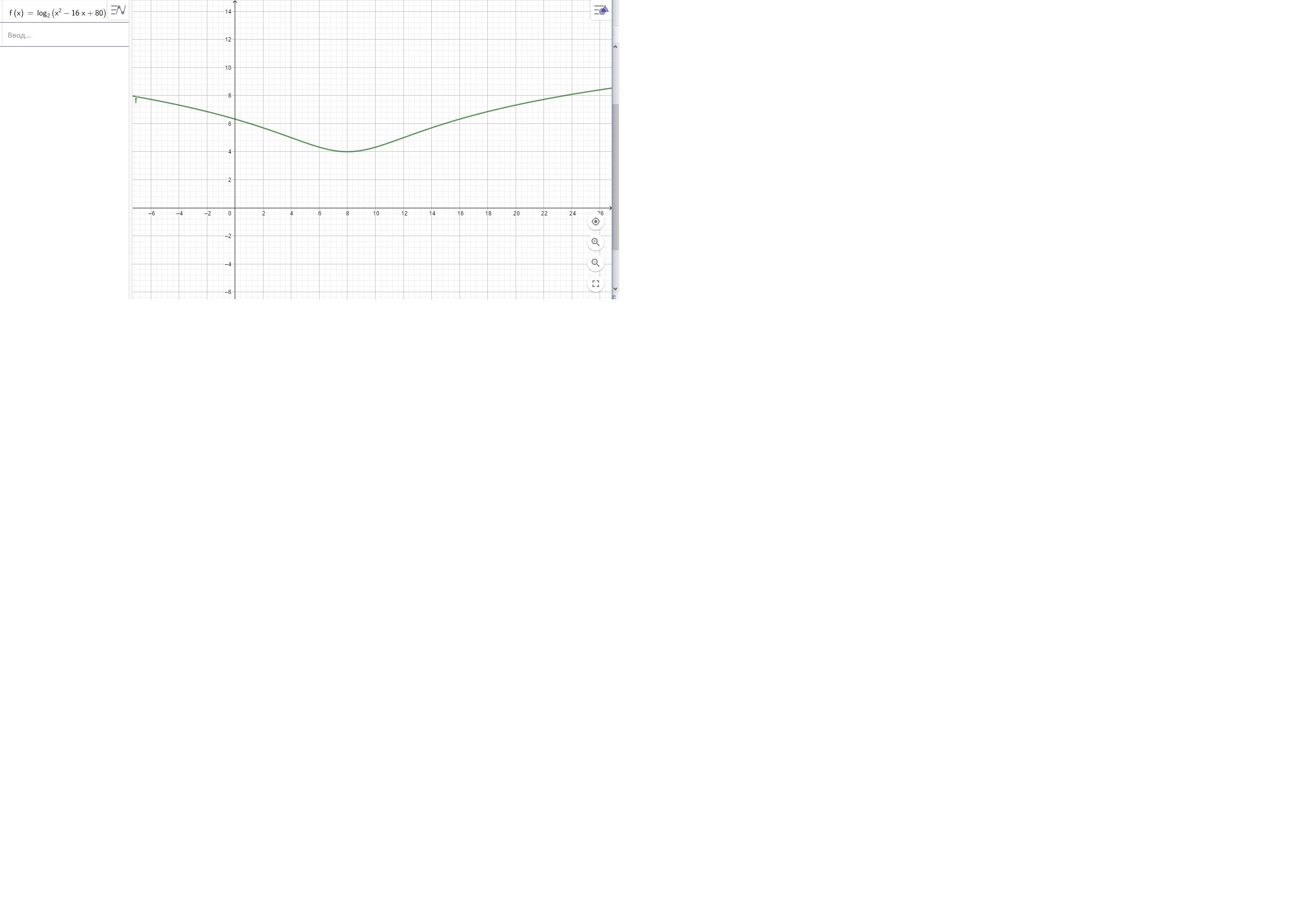
У подлогарифмического дискриминант отрицательный, значит оно никогда не обращается в 0

Наименьшее его значение в минимуме

-b/2a=16/2=8

Получается до 8 убывает, после 8 возрастает

У нас ограничение от 10 до 12

Значит 10 наименьшее