Question

срочно срочно срочно срочно

Answer 1

$2 sqrt{3} { (cos( frac{pi}{12} ) )}^{2} - sqrt{3} - 1 = sqrt{3} times (2 { (cos( frac{pi}{12} ) )}^{2} - 1) - 1 = \ \ = sqrt{3 } times cos( frac{ pi}{ 6 } ) - 1 = sqrt{3 } times frac{ sqrt{3} }{2} - 1 = frac{3}{2} - 1 = frac{1}{2} = 0.5$

Применил формулу:

$2 { (cos(x)) }^{2} - 1 = cos(2x)$



ОТВЕТ: 0,5

Answer 2

пожалуйста помогите https://znanija.com/task/29340833

Answer 3

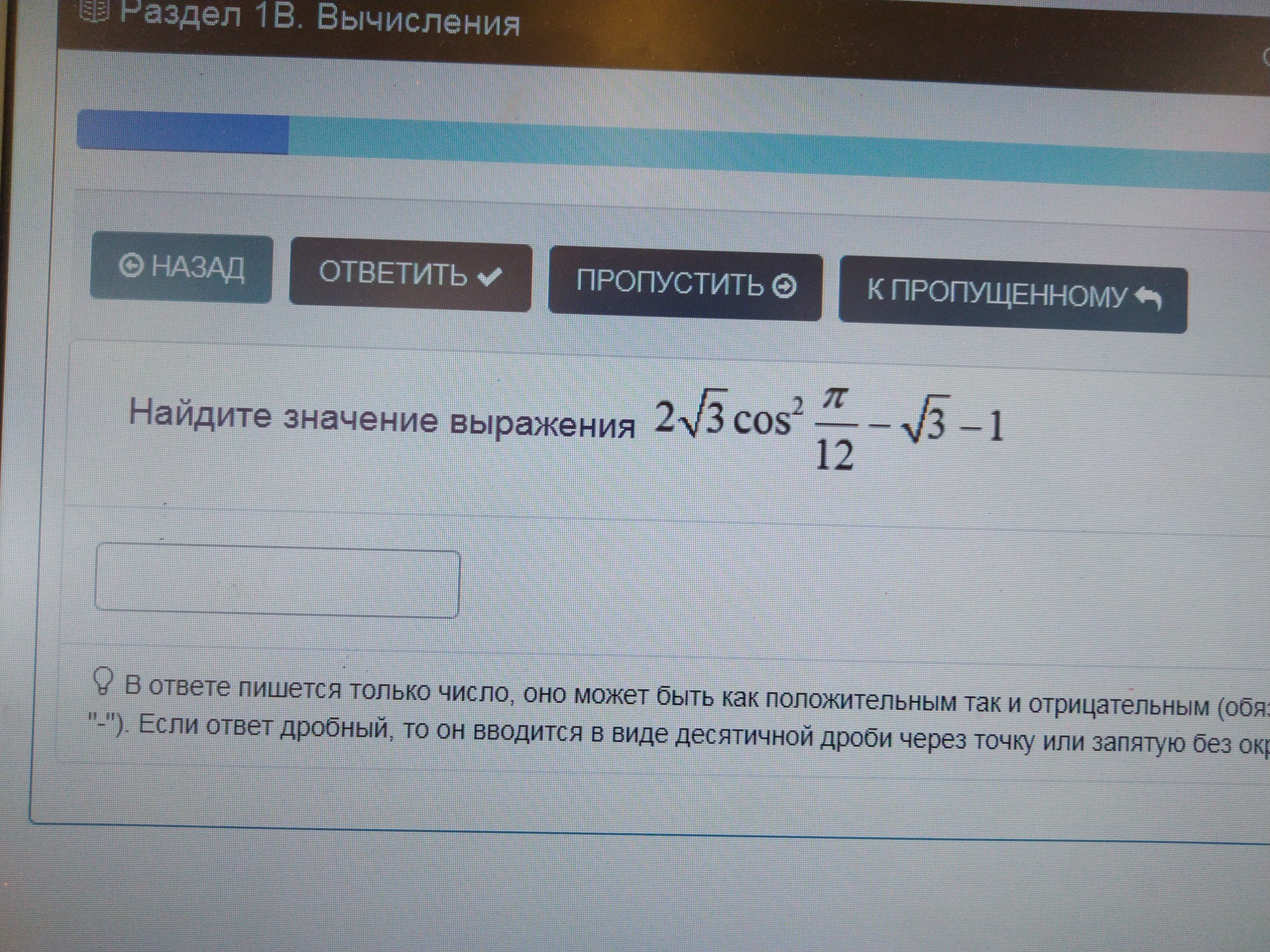
Используя формулу cos($frac{t}{2})=frac{1+cos(t)}{2}$,записать выражение в развёрнутом виде:

$2sqrt{3}*frac{1+cos(frac{pi}{6})}{2}-sqrt{3}-1$;

Вычислить выражение,используя таблицу значений тригонометрических функций:

$2sqrt{3}*frac{1+frac{sqrt{3}}{2}}{2}-sqrt{3}-1$;

Сократить числа на 2:

$sqrt{3}*(1+frac{sqrt{3}}{2})-sqrt{3}-1$;

Распределить $sqrt{3}$ через скобки:

$sqrt{3}+frac{3}{2}-sqrt{3}-1$;

Сократить противоположные выражения:

$frac{3}{2}-1$;

Вычислить разность:

$frac{1}{2}=0,5=2^{-1}$

Answer 4

пожалуйста помогите https://znanija.com/task/29340833