Question

Уравнение окружности с центром в точке пересечения графиков функций
y=$sqrt{5-x}$ и y=2 в степени Х
и радиусом r=1/2
Какой вид будет иметь уравнение?

Answer 1

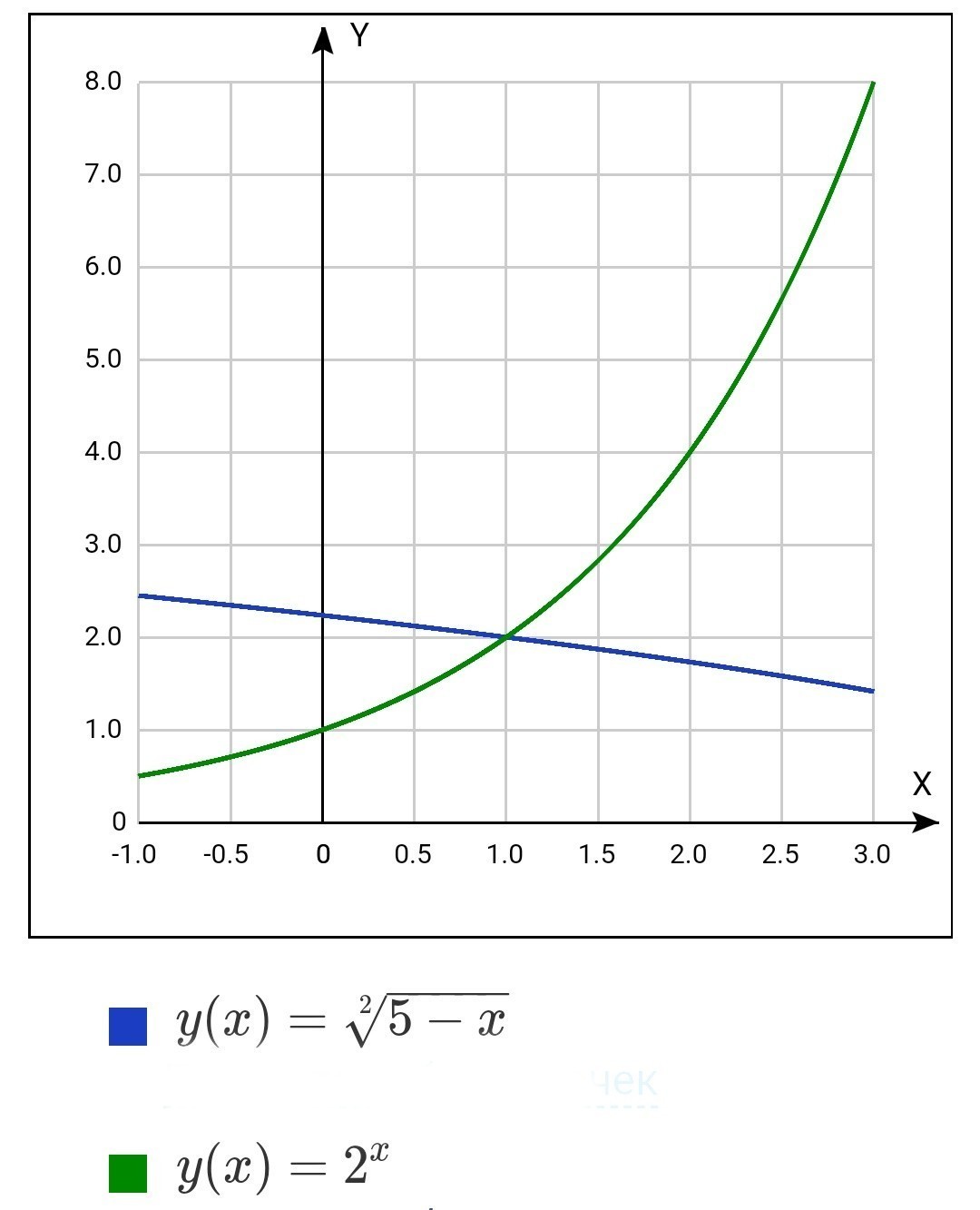
Решим уравнение
$sqrt{5 - x} = {2}^{x}$
Нетрудно видеть, что х=1
является решением данного уравнения
при этом у=2

других решений нет, потому что
$y1 (x)= sqrt{5 - x}$
убывающая на области допустимых значений, а
$y2 (x)= {2}^{x}$
возрастающая. (см также фото)

Итак центр окружности в (1,2), радиус ½

Уравнение имеет вид (х-1)²+(у-2)²= (1/2)²

Ответ
(х-1)²+(у-2)²=¼

Answer 2

А, почему х-1 и у-2 , а не х+1 и у+2 ???

Answer 3

потому что уравнение окружности имеет вид (x-xц)²+(у-уц)²=r²

Answer 4

Ясно, спасибо...