Question

Помогите пожалуйста и нужен рисунок

Answer 1

Каждая из заданных функций, является квадратичной (функцией вида y=ax^2+bx+c). Графиком квадратичной функции является парабола. Порядок построения параболы:
1. Находим координаты (х0, у0) вершины параболы:
x0=-b/(2a);
y0=y(x0)
2. Смотрим на коэффициент a (старший коэффициент): если он больше нуля, то ветви параболы смотрят вверх, если меньше - вниз.
3. Находим точки пересечения графика с осями координат.
4. Выбираем пару произвольных значений аргумента, находим соответствующие им значения функции.

Answer 2

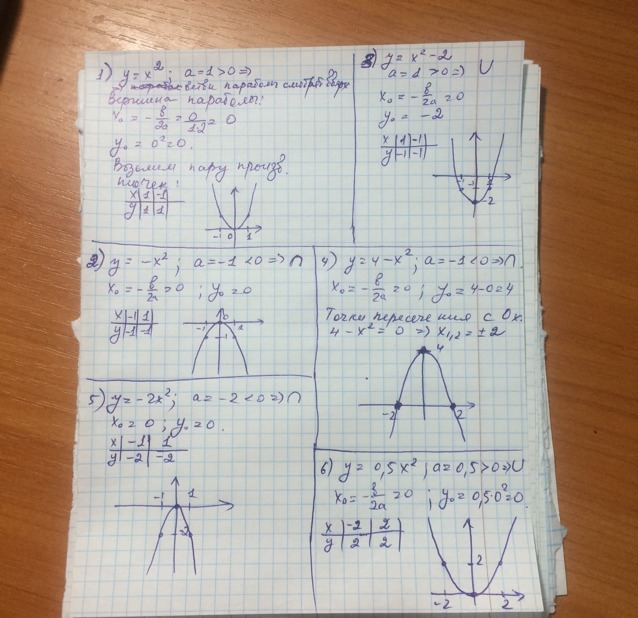
Задание состоит в построении графиков для уравнений вида y = ax² + bx + c. Ответ смотри в приложении.

Несколько простых правил построения графиков квадратичных функций:

1) Если a > 0, значит, ветви параболы направлены вверх, если же a < 0, то вниз.

2) Если c > 0, стандартный график (номер 1 в задании) поднимается вверх на c делений, если c < 0, график опускается на c.

3) При |a| > 1 (по модулю!), стандартный график сжимается, если же |a| < 1, график расширяется.

Т. н. "стандартный график" параболы легко строить по точкам (1; 1) и (2; 4). Начиная с точки (0; 0) проводим кривую через вышеназванные точки. По сути, любую параболу можно построить по нескольким простым точкам, но иногда быстрее использовать переносы.