Question

Помогите решить задание ОГЭ 2 части. 26 номер

Answer 1

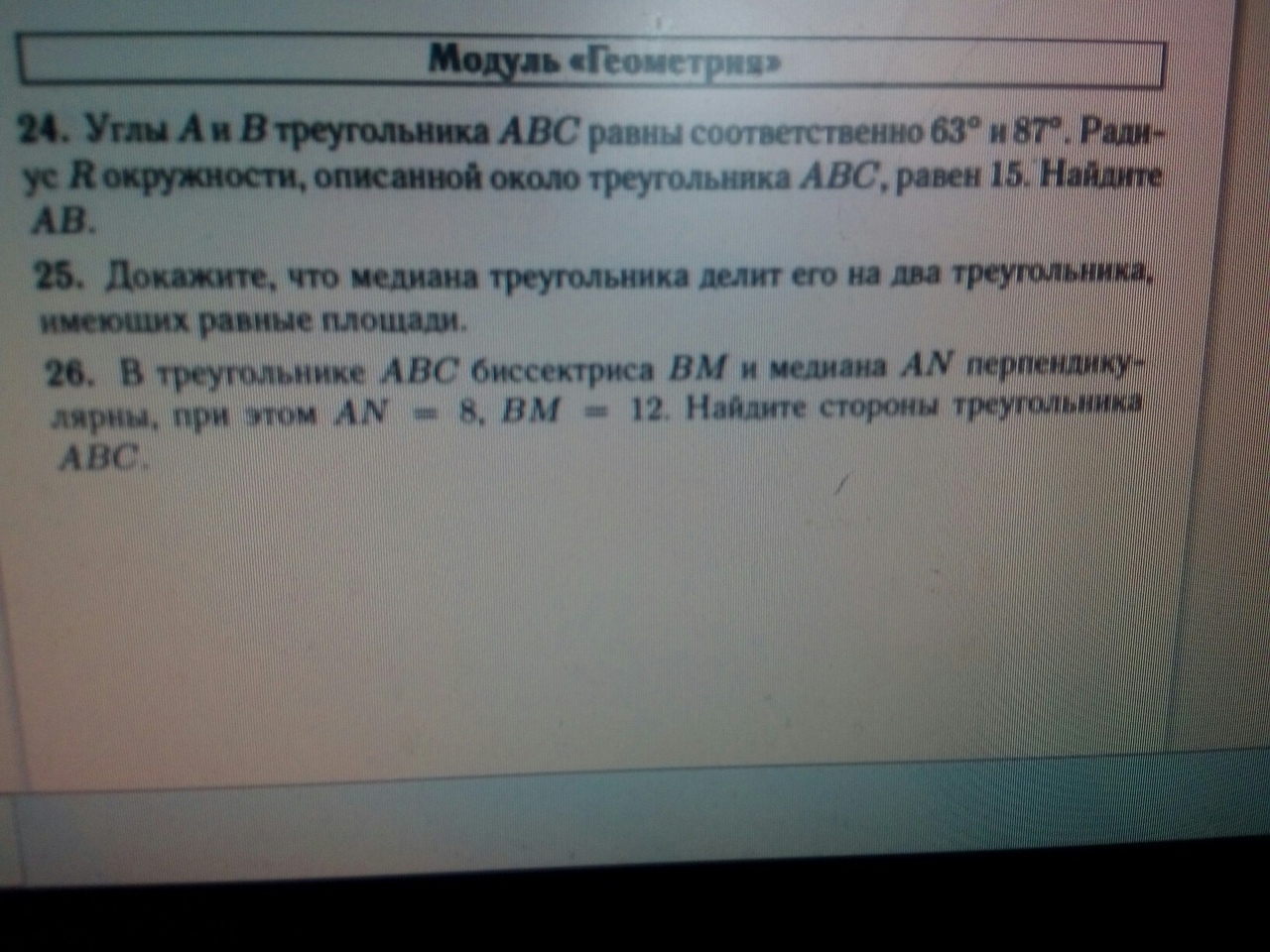
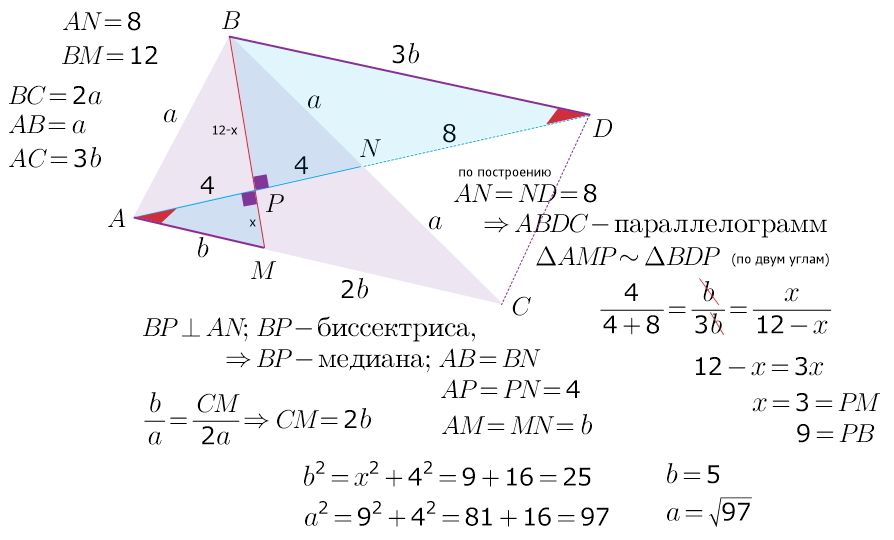
Если продолжить медиану треугольника на ее же длину, то можно достроить треугольник до параллелограмма (признак параллелограмма: диагонали точкой пересечения делятся пополам); это позволит рассмотреть два подобных прямоугольных треугольника...

по сути, будет доказан факт (можно назвать это и теоремой):

Если медиана ⊥ биссектрисе, то биссектриса точкой пересечения с медианой делится в отношении 3:1, считая от вершины.

остальное легко вычисляется: АВ = √97; ВС = 2√97; АС = 15

еще в решении использовалось свойство биссектрисы: биссектриса делит сторону треугольника на отрезки, пропорциональные прилежащим сторонам треугольника.

Answer 2

Можно просто сказать что авсд параллелограмм т.к. диагонали точкой пересечения делятся пополам

Answer 3

авДс порядок букв важен (в решении это написано...)

Answer 4

объясните почему АС=3в

Answer 5

потому что СМ=2b (по свойству биссектрисы)