Ответы
Ответ дал:
0
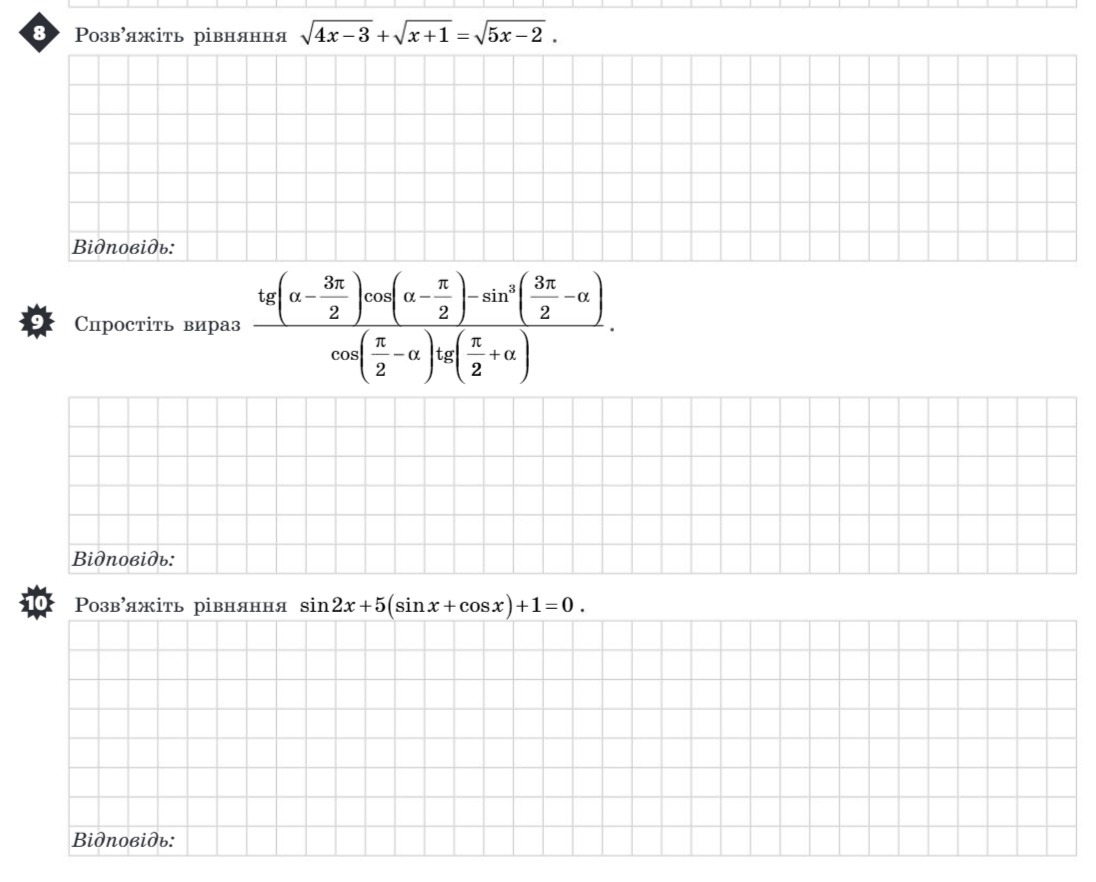
8.
Область определения:
1)
2)
3)
Значит,
Возведём в квадрат обе части уравнения и решим его:
Зная область определения, правильный ответ:
9.
Упростим выражение и получим:
Ответ: sin²α
10.
Ответ дал:
0
Извините, 10-е задание не знаю...
Ответ дал:
0
Дуже дякую і за це
Ответ дал:
0
Подставляем в формулу:
Выносим общий множитель ( sinx + cosx ):
Произведение равно нулю только тогда, когда хотя бы один из множителей равен нулю
Разделим обе части уравнения на соsx ≠ 0 :
n € Z
Вынесем за скобку √2 и в скобке можно заметить синус суммы:
Так как значения синуса принадлежат промежутку от - 1 до 1
Значит, здесь нет корней
ОТВЕТ: - π/4 + πn, n € Z
Вас заинтересует
3 года назад
9 лет назад