Question

Срочно, найти площадь заштрихованной области.

Answer 1

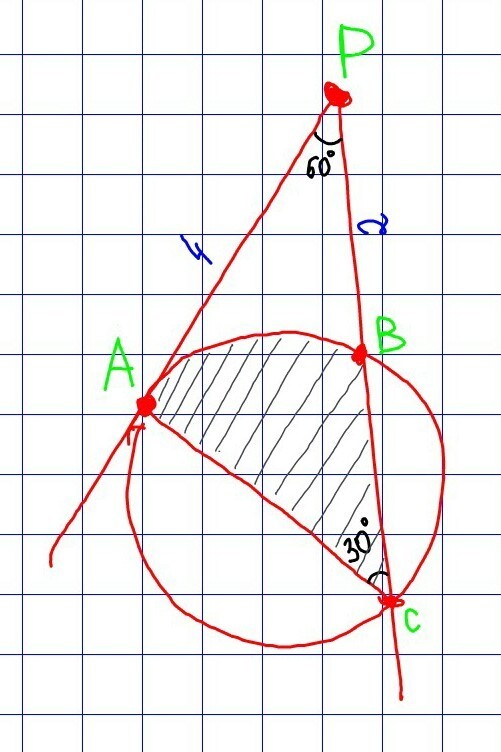
1) угол PAB = угол АСВ = 30° - по теореме угла между касательной и хордой

угол АРВ + угол РАВ = 60° + 30° = 90°

Значит, ∆ АРВ и ∆ АВС прямоугольные =>

АС - диаметр окружности, так как прямой угол в окружности всегда опирается на диаметр окружности

2) Рассмотрим ∆ РАС :

Катет, лежащий против угла в 30°, равен половине гипотенузы =>

РС = 2 × АР = 2 × 4 = 8

ВС = РС - РВ = 8 - 2 = 6

3) Рассмотрим ∆ РАВ:
По теореме Пифагора:

АВ² = 4² - 2² = 16 - 4 = 12

АВ = 2√3

4) Рассмотрим ∆ АВС:

Катет, лежащий против угла в 30°, равен половине гипотенузы =>

АС = 4√3

АО = ОС = 2√3 - радиусы окружности

5) Площадь сектора АОВ равна:

S = πR² × a / 360° = π × ( 2√3 )² × 60° / 360° = 2π

a = угол АОВ

6) Площадь ∆ ВОС:

S = abc / 4R = ( 2√3 × 2√3 × 6 ) ÷ ( 4 × 2√3 ) = 3√3

В итоге площадь заштрихованной области равна:

S = 2π + 3√3

ОТВЕТ: 2π + 3√3

Answer 2

Спасибо большое, четко изложили

Answer 3

Только площадь сектора 2п

Answer 4

Да, Вы правы

Answer 5

Ха, в уме считать не умею ))

Answer 6

бывает) спасибо еще раз))

Answer 7

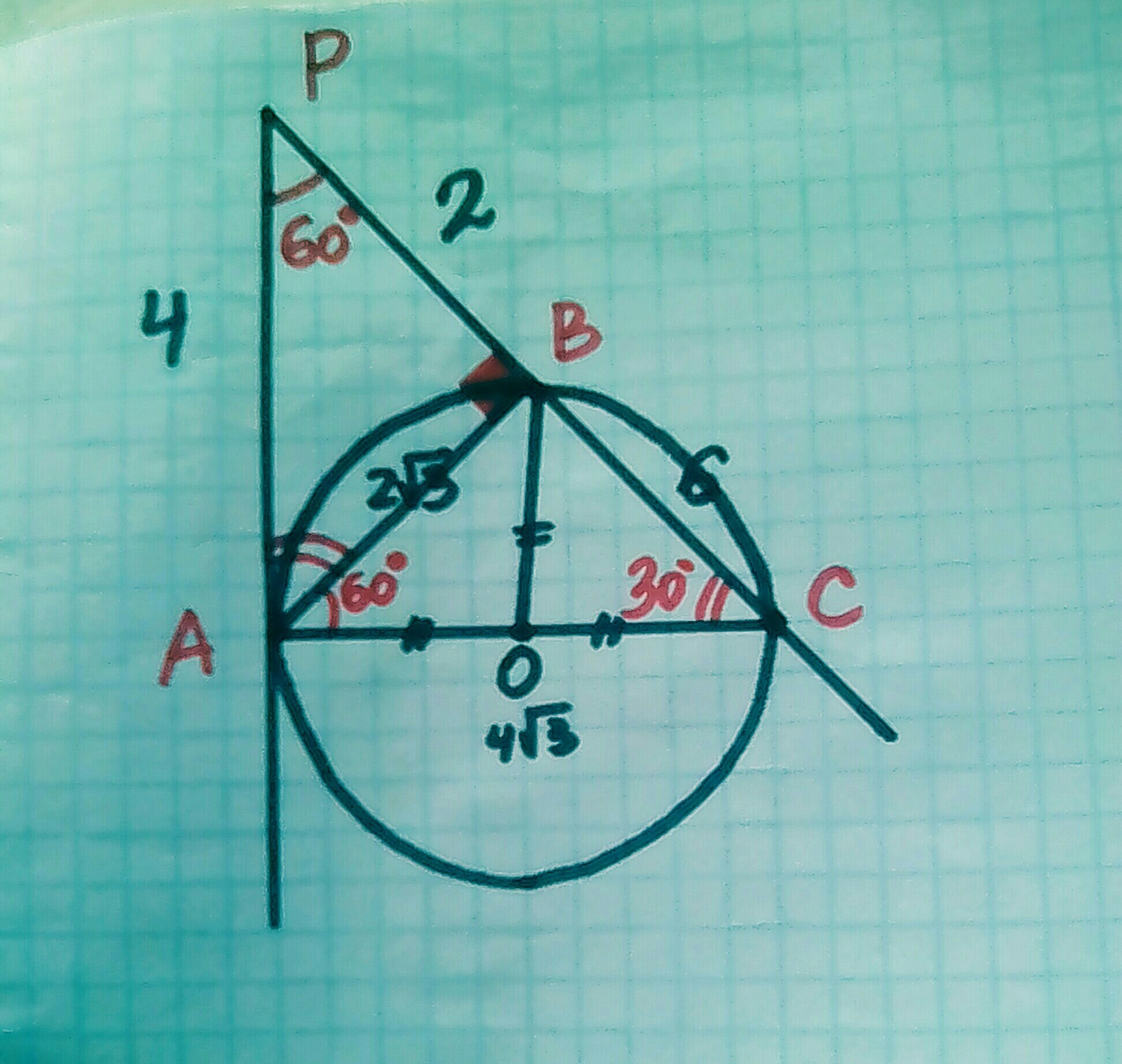
<CAP=90°
РС гипотенуза
РС=2•АР=2•4=8
ВС=РС-РВ=8-2=6
по теорема Пифагора
АС²=64-16=48
АС=4√3
по теорема косинуса
АВ²=48+36-2*4√3*6*cos30°=
48+36-72=12
AB=2√3
по теорема синуса
AB/sin30°=2R
2R=2√3:1/2=2√3*2=4√3
R=2√3
<АОВ=60°
S1=(πR²/360°)*60°=
(π•12/360°)*60=2π
O центр окружность
вписанной ∆ ВАС

S(BOC)=2√3•6•sin30°*1/2=
3√3
S=S1+S(BOC)=2π+3√3

Answer 8

Напоминает площадь сектора, но и там на 60 градусов домножать.

Answer 9

там 30°

Answer 10

Заштрихованная область не является сектором. Разделить на части и сложить площади каждой части, как в ответе выше, куда правильнее

Answer 11

огромное спасибо

Answer 12

вам спасибо)