Расстояние от точки до плоскости
В прямой треугольной призме ABCDA1B1C1 известны ребра AB=BC=1, AC=√2, AA1=1. Найдите расстояние от точки B1 до плоскости A1BC1
Ответы
Ответ дал:
0
Из задания следует, что основание призмы - равнобедренный прямоугольный треугольник.
Искомое расстояние - это перпендикуляр из точки В1 к плоскости А1ВС1.
Он лежит в плоскости, перпендикулярной ребру А1С1, проходящей через ребро ВВ1.
Проведём такое сечение призмы.
В сечении прямоугольник Д1В1ВД высотой 1 и с основанием, равным половине АС.
Находим диагональ Д1В, в которую из точки В1 опустим перпендикуляр.
Д1В = √(1² + (√2/2)²) = √(1 + (2/4)) = √(3/2).
Отсюда находим искомую длину L как отрезок В1К:
L = ((√2/2)*1) / (√(3/2)) = 1/√3 = √3/3.
Приложения:
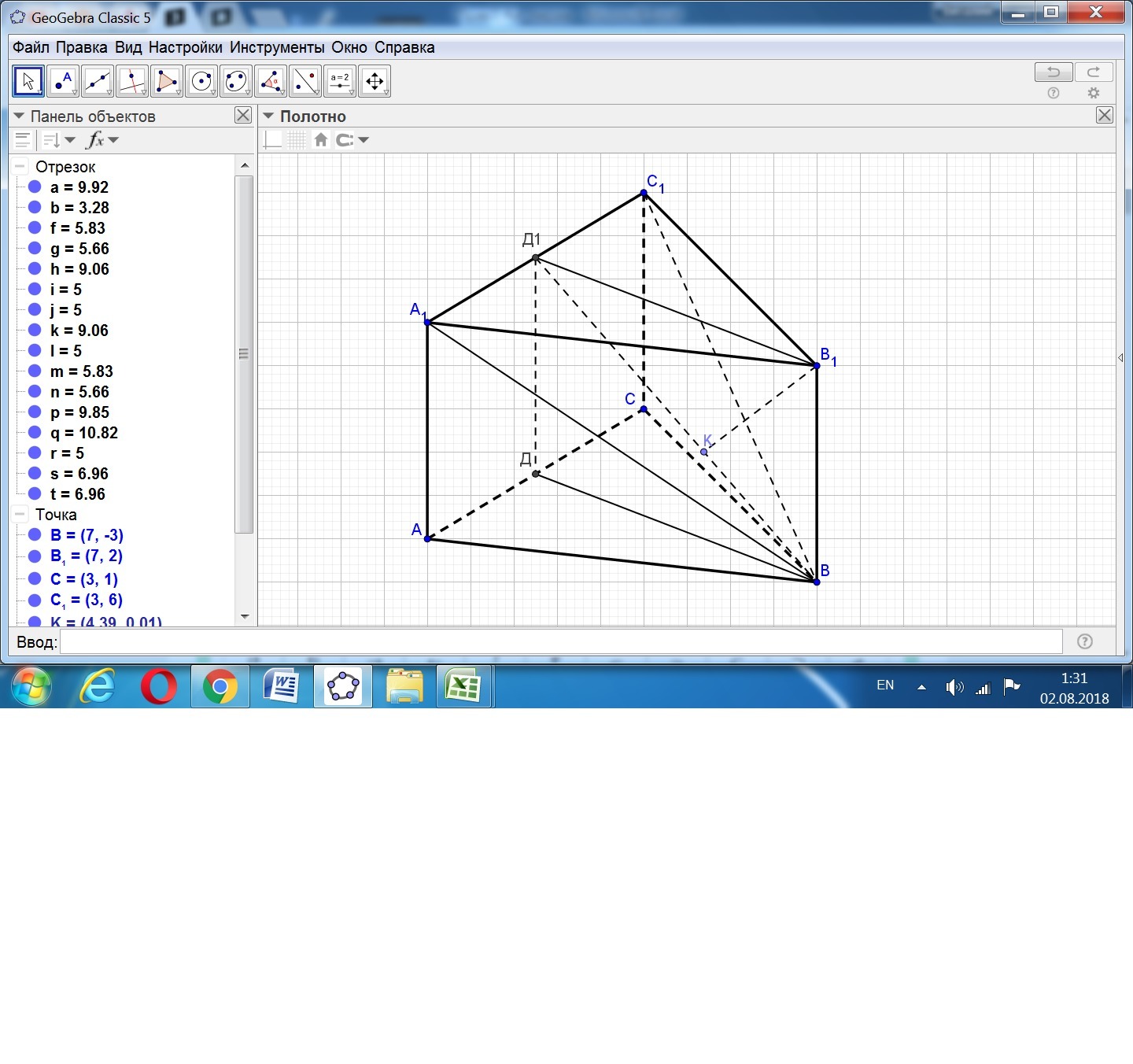
Ответ дал:
0
Всё предельно понятно, спасибо!
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад