Question

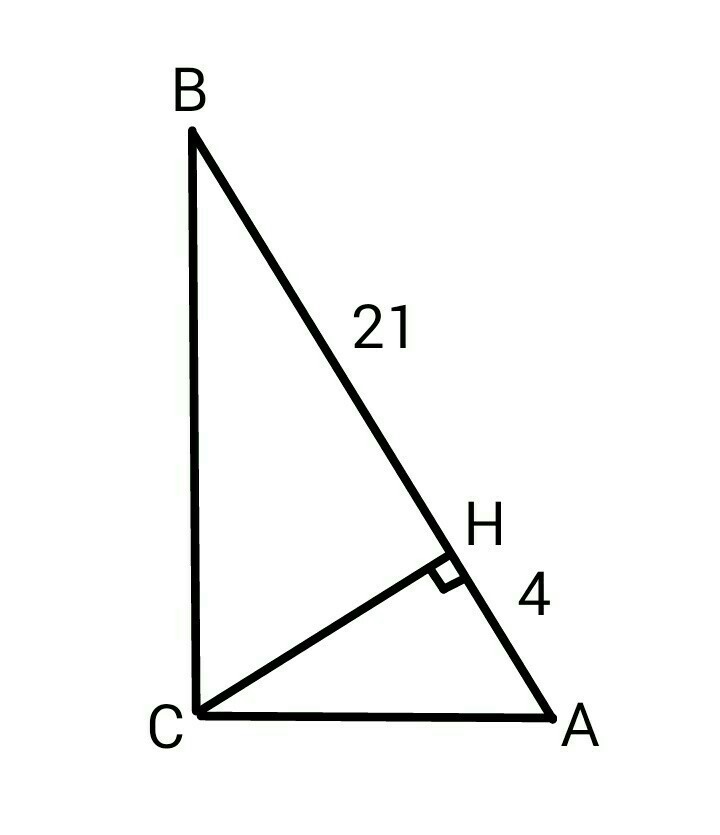
Дано : треугольник ABC прямоугольный, угол C = 90°, опущена высота CH на гипотенузу AB.
Найти катеты ABC , если их проекции равны 4 и 21.

Answer 1

Напишем систему уравнений в соответствии с теоремой Пифагора:
${bc}^{2} = {21}^{2} + {ch}^{2} \ {bc}^{2} = {25}^{2} - {ac}^{2} \ {ac}^{2} = {4}^{2} + {ch}^{2} \ {ac}^{2} = {25}^{2} - {bc}^{2}$
Решаем систему уравнений:
${bc}^{2 } = {21}^{2} + {ac}^{2} - {4}^{2} = \ = {21}^{2} + {25}^{2} - {bc}^{2} - {4}^{2} \ bc = sqrt{ frac{ {21}^{2} + {25}^{2} - {4}^{2} }{2} } = sqrt{525}$
${ac}^{2} = {4}^{2} + {bc}^{2} - {21}^{2} = \ = {4}^{2} + {25}^{2} - {ac}^{2} - {21}^{2} \ ac = sqrt{ frac{ {4}^{2} + {25}^{2} - {21}^{2} }{2} } = sqrt{100} = 10$
Ответ: катет bc = √525; катет ac = 10

Answer 2

Самый лёгкий способ: вспомните тему " пропорциональные отрезки в прямоугольном треугольнике " и задача будет решаться в два действия....

Answer 3

а мы пойдем другим , более легким, путем

решение смотри в файле