Question

Решите пожалуйста пятый номер из фото.

Answer 1

Уравнение окружности имеет вид:

$(x-x_{0})^2+(y-y_{0})^2=R^2$, где $(x_{0};y_{0})$ - центр окружности, $|R|$ - её радиус

График "уголка" имеет вид:

$y=k|x-x_{0}|+b$, где $(x_{0};b)$ - вершина, а k - угол наклона ветвей

Строим графики:

$(x-0)^2+(y-0)^2=1^2$ - окружность с центром в точке (0; 0) и радиусом |1|=1

$y=-|x|+a$ - угол наклона $tg(alpha)=-1$, откуда $alpha=135$ (градусов)

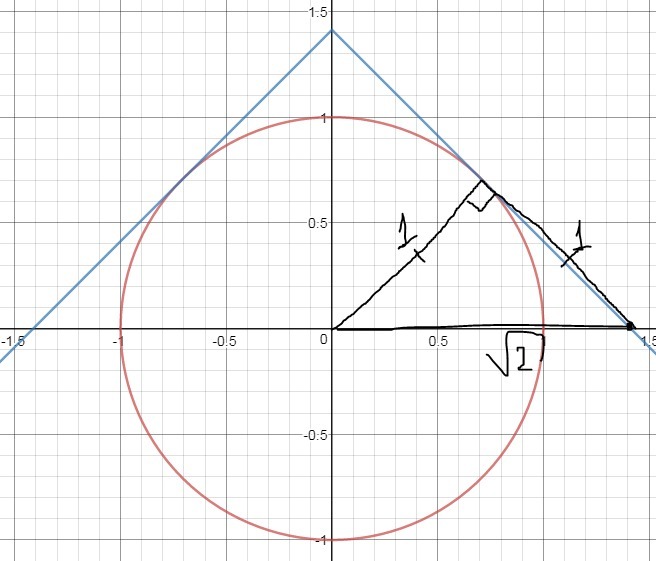
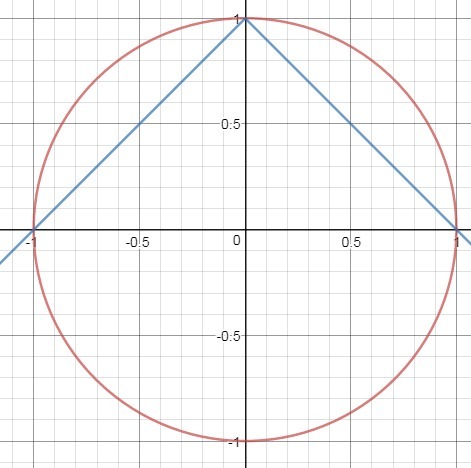
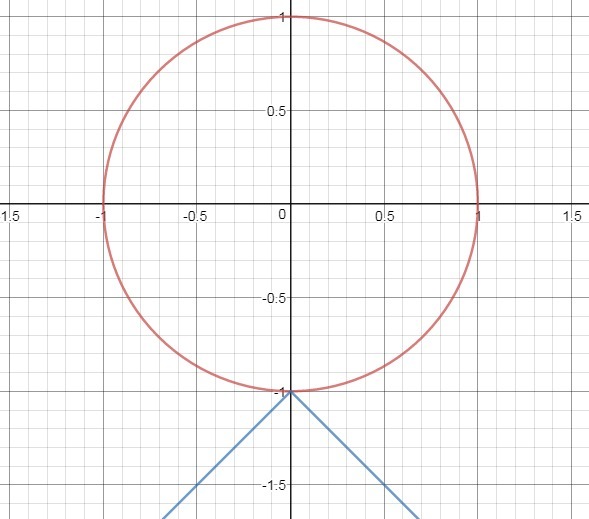
Далее чертим (см. рис.)

2 решения:

1 случай: касание (равнобедр. треугольник, сразу находим a) $a=sqrt{2}$

2 случай: вершина на окружности: a=1

3 случай: "уголок" за окружностью: a=-1

Ответ: $-1<a<1$ или $a=sqrt{2}$

Answer 2

А где рисунок?

Answer 3

И почемумв ответе только -1?

Answer 4

забыл рисунок прикрепить, а в ответе было всё нормально итак