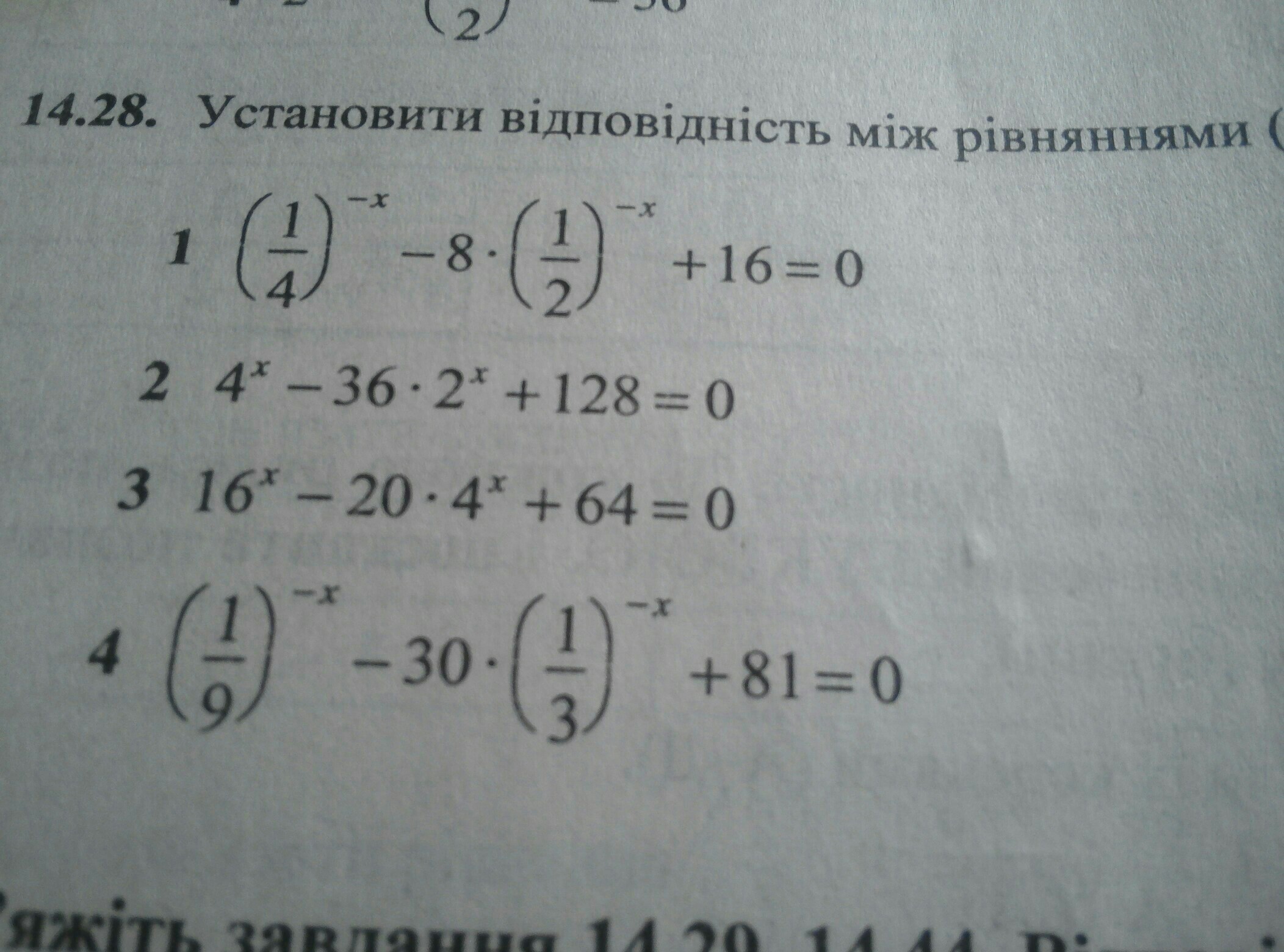Ответы
Ответ дал:
0
Из этого видно, что здесь присутствует формула:
( a - b )² = a² - 2ab + b²
ОТВЕТ: 2
Расложим на множители
ОТВЕТ: 2 ; 5
Разложим на множители:
ОТВЕТ: 1 ; 2
Разложим на множители:
ОТВЕТ: 1 ; 3
Вас заинтересует
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад