Question

|3x-4|+|5x-6|<2

Решал с помощью общего метода решения неравенств с модулем и получился такой ответ: x принадлежит (1; 6/5) ; (6/5; 4/3) ; ( 4/3; 3/2 ). Но правильный ответ (1; 3/2)

Что не так у меня?

Answer 1

найдем корни уравнения: |3x-4|+|5x-6|=2

Для этого рассмотрим 3 случая

Сначала найдем нули подмодульных выражений:

$1) 3x-4=0 \ \ x=frac{4}{3} \ \ 2) 5x-6=0 \ \ x=frac{6}{5}$

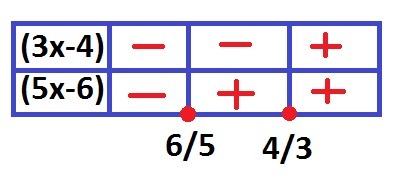
знаки, с которыми раскроется модуль удобно представить в таблице (см. рисунок)

1 случай)

$left{begin{matrix}x<frac{6}{5} \ \ -(3x-4)-(5x-6)=2end{matrix}right. Leftrightarrow left{begin{matrix}x<frac{6}{5} \ \ -3x+4-5x+6=2end{matrix}right. Leftrightarrow left{begin{matrix}x<frac{6}{5} \ \ 8x=8end{matrix}right. Leftrightarrow \ \ \ Leftrightarrow left{begin{matrix}x<frac{6}{5} \ \ x=1 end{matrix}right. Leftrightarrow x=1$

2 случай)

$left{begin{matrix}frac{6}{5}leq x leqfrac{4}{3} \ \ -(3x-4)+(5x-6)=2end{matrix}right. Leftrightarrow left{begin{matrix} frac{6}{5}leq x leq frac{4}{3}\ \ -3x+4+5x-6=2end{matrix}right. Leftrightarrow left{begin{matrix} frac{6}{5}leq x leqfrac{4}{3} \ \ 2x=4end{matrix}right. \ \ \ Leftrightarrow left{begin{matrix} frac{6}{5}leq x leqfrac{4}{3} \ \ x=2 end{matrix}right. Leftrightarrow x in varnothing$

3 случай)

$left{begin{matrix}x > frac{4}{3} \ \ (3x-4)+(5x-6)=2end{matrix}right. Leftrightarrow left{begin{matrix} x > frac{4}{3} \ \ 3x-4+5x-6=2end{matrix}right. Leftrightarrow left{begin{matrix} x > frac{4}{3} \ \ 8x=12end{matrix}right. Leftrightarrow \ \ \ Leftrightarrow left{begin{matrix} x > frac{4}{3} \ \ x=frac{3}{2} end{matrix}right. Leftrightarrow x=frac{3}{2}$

в итоге из 3-х случаев получаем 2 корня: 1 и 3/2

Наносим их на координатную прямую (метод интервалов):

|3x-4|+|5x-6|<2

|3x-4|+|5x-6|-2<0

+++(1)---(3/2)+++>x

$OTBET: x in (1; frac{3}{2} )$