Question

Даны две концентрические окружности. Хорда большой окружности имеет длину 40 см и касается меньшей окружности. Найти радиус большой окружности , если ширина кольца между этими окружностями равна 10 см

Answer 1

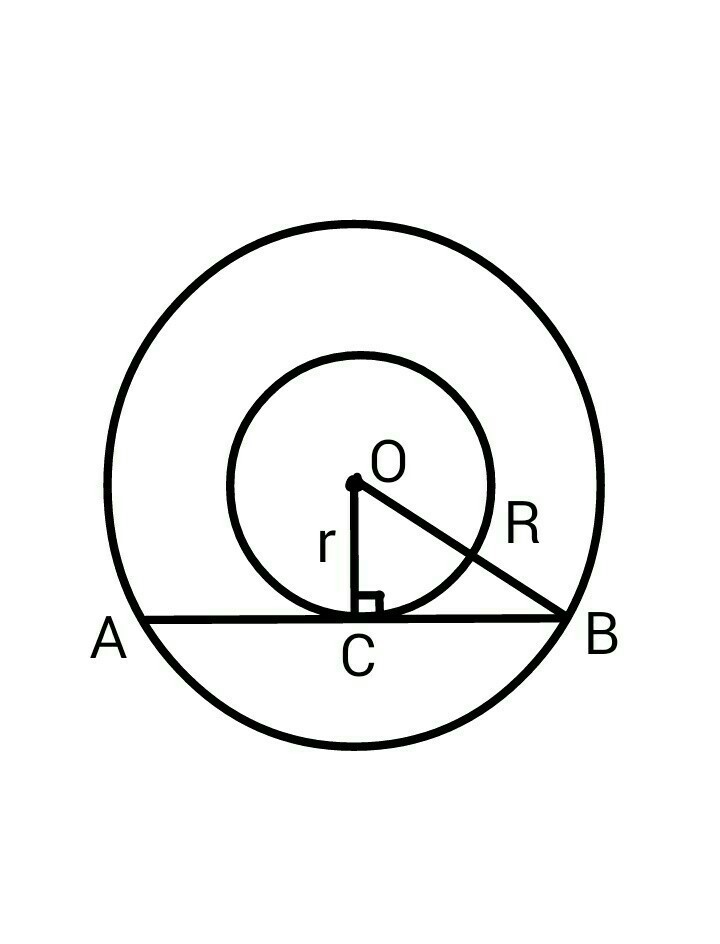
CB = AB/2 = 40/2 = 20
Из треугольника COB:
OB^2 = OC^2 + CB^2
R^2 = r^2 +20^2
Понятно, что:
R - r = 10
Получаем систему уравнений:
R^2 = r^2 +20^2 (1)
R - r = 10 (2)
Из уравнения (2) r = R - 10
Подставляем в уравнение (1):
R^2 = (R - 10)^2 + 400 = R^2 - 20R + 100 + 400
Сокращаем, и получаем:
20R = 500
R = 25 см
Ответ: радиус большей окружности R = 25 см