Question

Здравствуйте, подскажите, как решить уравнение, желательно подробно, заранее спасибо!

Answer 1

7/(x ² - 9)≥ 1
7/(x² - 9)- 1≥ 0
(7 - x² + 9)/ (x²- 9)≥0
(16 - x²)/(x² - 9) ≥0
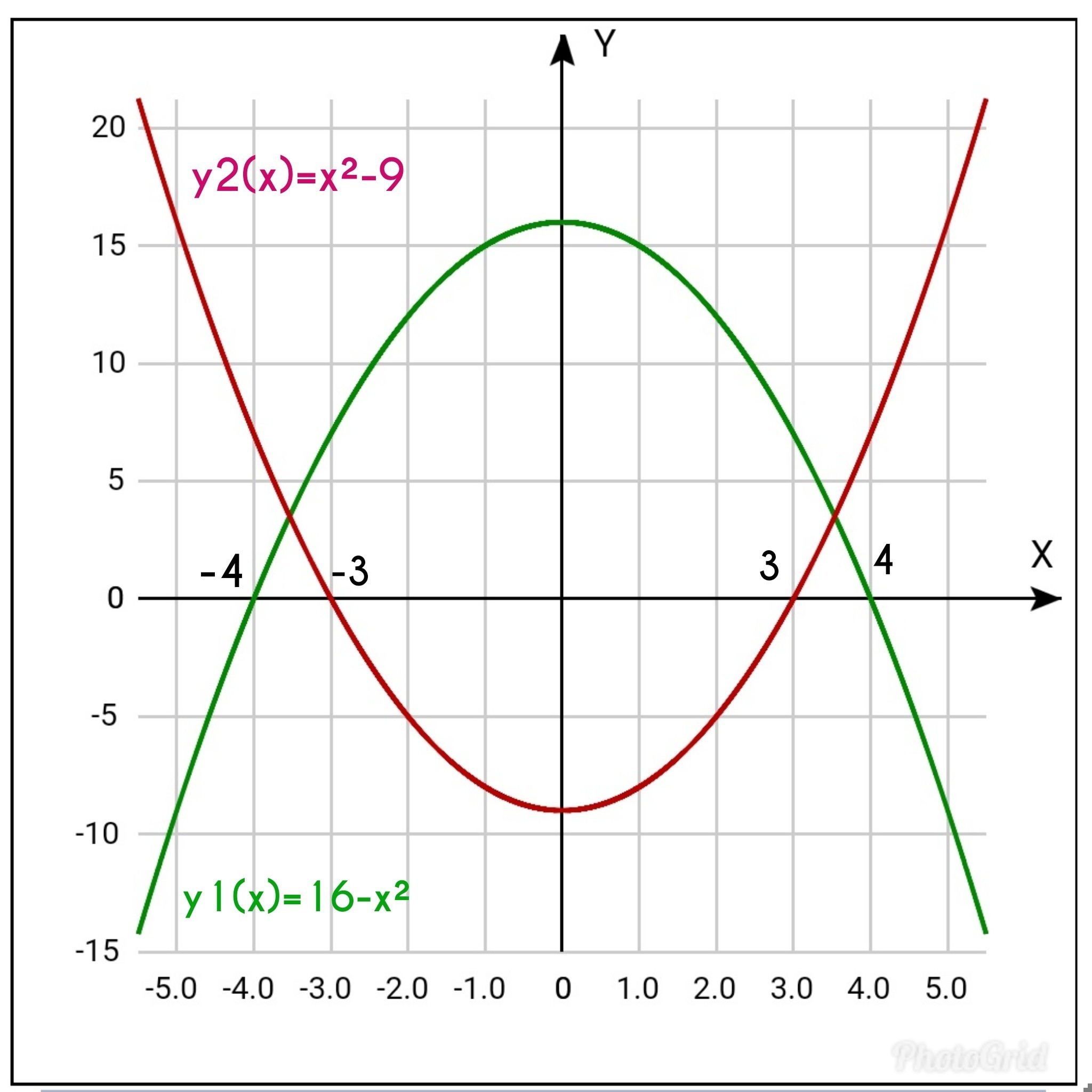
построим графики
y1(x)=16-x² и y2(x)=x²-9 (см фото)
их легко построить, если взять за основу параболу х².

Наше неравенство будет соблюдено , если y1 (x)и у2(x) будут одного знака,
откуда получаем решение ( с учётом области определения x²-9≠0 или х≠±3)

x€[-4, -3)v(-3, 4]

Получаем, что целочисленные решения будут
-4, +4
Их два
Ответ (1) два решения

удачи Вам!

Answer 2

Большое спасибо, через параболы намного проще решить это уравнение, я решал методом интервалов и запутался в ответах всего навсего)

Answer 3

$frac{7}{x^2-9}geq 1; ,quad frac{7}{x^2-9}-1geq 0; ,quad frac{7-x^2+9}{x^2-9}geq0; ,quad frac{-x^2+16}{x^2-9}geq 0\\frac{-(x-4)(x+4)}{(x-3)(x+3)}geq 0; quad frac{(x-4)(x+4)}{(x-3)(x+3)}leq 0\\znaki:; ; ; +++[-4, ]---(-3)+++[, 4; ]---(3)+++\\xin [-4,-3)cup [, 4,3)\\celue; reshenija:; ; x=-4; ,; x=4$

Ответ: два целочисленных решения.

Answer 4

опечатка: промежуток не по порядку написан)) (3; 4] (у меня тоже так бывает...))

Answer 5

Спасибо за помощь)