Question

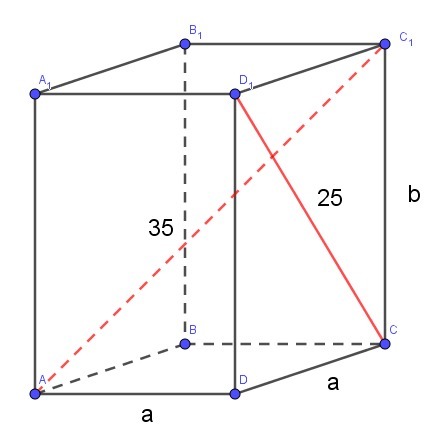
диагональ правильной четырехугольной призмы равна 35 дц, а диагональ боковой грани равна 25 дц. вычислите объем призмы

Answer 1

Если четырехугольная призма правильная, то в основании лежит квадрат!

Пусть а - сторона квадрата, b-высота призмы, тогда

$AC_1^2=AD^2+CD^2+CC_1^2 \ 35^2=a^2+a^2+b^2 \ 2a^2+b^2=1225 \ \ DC_1^2=CD^2+CC_1^2 \ 25^2=a^2+b^2 \ a^2+b^2=625$

получаем систему:

$left { {{2a^2+b^2=1225} atop {a^2+b^2=625}} right.$

вычтем из первого второе:

$a^2=600 \ a=sqrt{600}=10sqrt{6} \ \ a^2+b^2=625 \ 600+b^2=625 \ b^2=25 \ b=5 \ \ V=a*a*b=a^2*b=600*5=3000$

Ответ: 3000 дм³