Question

17 баллов) Найдите сторону треугольника ВС, если АС равно 12 см, АВ=6 см, а биссектриса внешнего угла при вершине А пересекается со стороной СВ в точке К и ВК=8 см.

Answer 1

∠BAD - внешний углол при вершине А

Дополнительные построения:

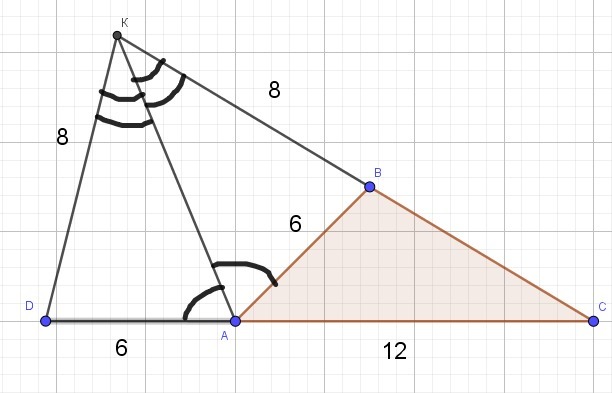
отложим отрезок АD=6 см и соединим точки К и D

Теперь рассмотрим треугольники ADK и ABK

AD=AB - по построению

АК - общая; ∠DAK=∠BAK - так как АК - биссектриса (по условию)

Следовательно ΔADK=ΔAВK - по 1-му признаку ⇒ KD=KB=8; ∠DKA=∠AKB, значит в ΔDKC: AK-биссектриса

По свойству биссектрисы:

$frac{AC}{AD} =frac{CK}{DK} \ \ frac{12}{6} =frac{CK}{8} \ \ CK=16\ \ BC=CK-KB=16-8=8$

Ответ: 8 см