Question

С точки к оркужности проведены 2 касательные. Каждые из них равны 15 см, а расстояние между касатаельными равно 24 см . Найдите длину окружности ?

Answer 1

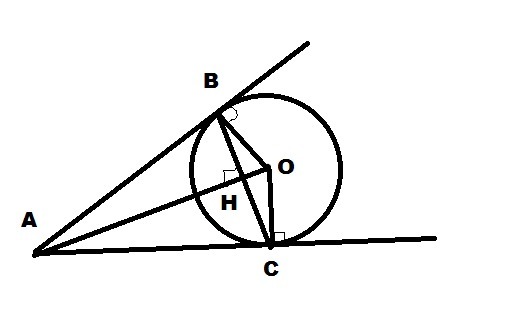
Пусть касательные проведены из точки А, а

С и В - точки касания.

По условию АВ=АС=15

ВС=24

АВС - равнобедренный треугольник.

Соединим А и центр О.

Треугольник ВОС равнобедренный.

АН - высота треугольника ВАС.

ОН - высота треугольника ВОС.

ВН=24:2=12

Из ⊿АНВ по т.Пифагора находим АН=9

OВ=r

Рассмотрим прямоугольный треугольник АВО.

ОН в нем - высота.

Высота прямоугольного треугольника, проведенная из вершины 

прямого угла, есть среднее пропорциональное между отрезками, 

на которые делится гипотенуза этой высотой

АН=9.

ВН²=9 ОН

144=9 ОН

ОН=16

Из прямоугольного треугольника ВНО:

ОВ²=ОН²+ВН²

OB=r

r²=16²+12²

r²=256+144=400

r=20

L(окружности)=2*$pi$*r

L=2*$pi$*20=40*$pi$

Ответ:40$pi$

Answer 2

см рисунок.

пусть ∠BAH = α, тогда ∠ABH = 90° - α, ∠HBO = α => треугольник ABH подобен треугольнику HBO

Отсюда:

$frac{AB}{BO} = frac{BH}{OH} \\ frac{15}{r} =frac{12}{OH}\\ OH=0,8r$

в треугольнике HBO по теореме Пифагора:

r² = 12² + (0,8r)²

(0,6r)² = 12²

0,6r = 12

r = 20 (см)

L = 2πr = 2*20π = 40π (cм)

Ответ: 40π см