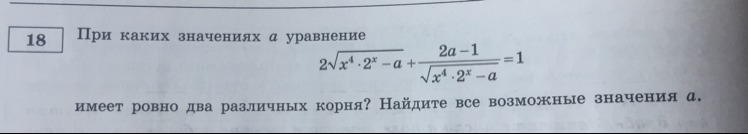Question

25 баллов даю РЕШИТЕ ПОЖАЛУЙСТА. Ответ будет (0,5;9/16)

Answer 1

√(х⁴*2^x -a) = t

2t +(2a -1)/t =1 | *t

2t² -t +(2a -1)= 0, ⇒ D = 1-4*2*(2a-1) = 9 -16a

t≠ 0,

(х⁴*2^x -a) > 0 , х⁴*2^x > a, ⇒ a < х⁴*2^x,⇒ a > 0,5 ( по графику )

Чтобы уравнение имело 12 корня, надо, чтобы дискриминант был >0

9 - 16a > 0, ⇒ a < 9/16

Ответ: (0,5; 9/16)

Answer 2

и с чего это функция x^4 * 2^x > 0.5? при 0.5 3 пересечения, а предел только в нуле...

Answer 3

Да, тут есть косяк. Надо было написать, что t всегда больше нуля (из ОДЗ уравнения и области определения корня). Далее когда посчитан дискриминант, меньший из корней будет равен 1/4 - √(9/16 - a)... t всегда больше нуля, отсюда условие на меньший корень 1/4 - √(9/16 - a)>0 откуда 1/2 < a <= 9/16. Равенство 9/16 отпадает из строгой положительности дискриминанта, так вот и получается ответ.

Answer 4

это следует из уравнения для t, верно. 2t^2-t+2a-1=0; 2(t^2+a)=t+1, t^2+a>1/2. По корням сложно смотреть, так как у функции x^4*2^x производная нулю равна в точке (-4)/(ln2)