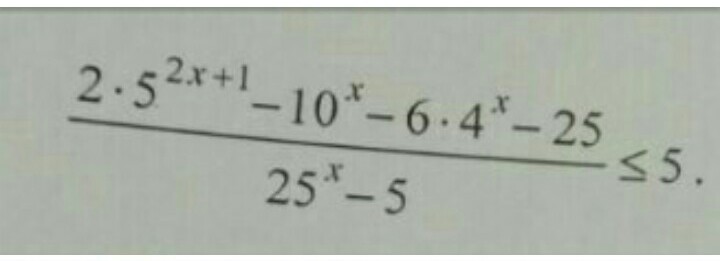Question

помогите!!!!!!!!!!!!!!!!!!!!!!!!

Answer 1

5²ˣ⁺¹=5·(5ˣ)²

(10·(5ˣ)²-2ˣ·5ˣ -6·(2ˣ)²-25-5·(5ˣ)²+25)/((5ˣ)²-5)≤0

(5·(5ˣ)²-2ˣ·5ˣ -6·(2ˣ)²)/((5ˣ)²-5)≤0

(5ˣ+2ˣ)(5·5ˣ -6·2ˣ)/((5ˣ)²-5)≤0

5ˣ+2ˣ>0 при любом х

Решаем методом интервалов неравенство

(5·5ˣ -6·2ˣ)/((5ˣ)²-5)≤0

Нули числителя:

(5·5ˣ -6·2ˣ)=0

(5/2)ˣ=6/5

х=log₂,₅ 1,2

Нули знаменателя:

(5ˣ)²-5=0

5²ˣ=5

2х=1

х=0,5

_+_ [log₂,₅ 1,2] __-__ (0,5) _+__

log₂,₅ 1,2 <log₂,₅ sqrt(2,5)=log₂,₅ (2,5)⁰,⁵=0,5

О т в е т. [log₂,₅ 1,2; 0,5)

Answer 2

Спасибо тебе!

Answer 3

..........,...............