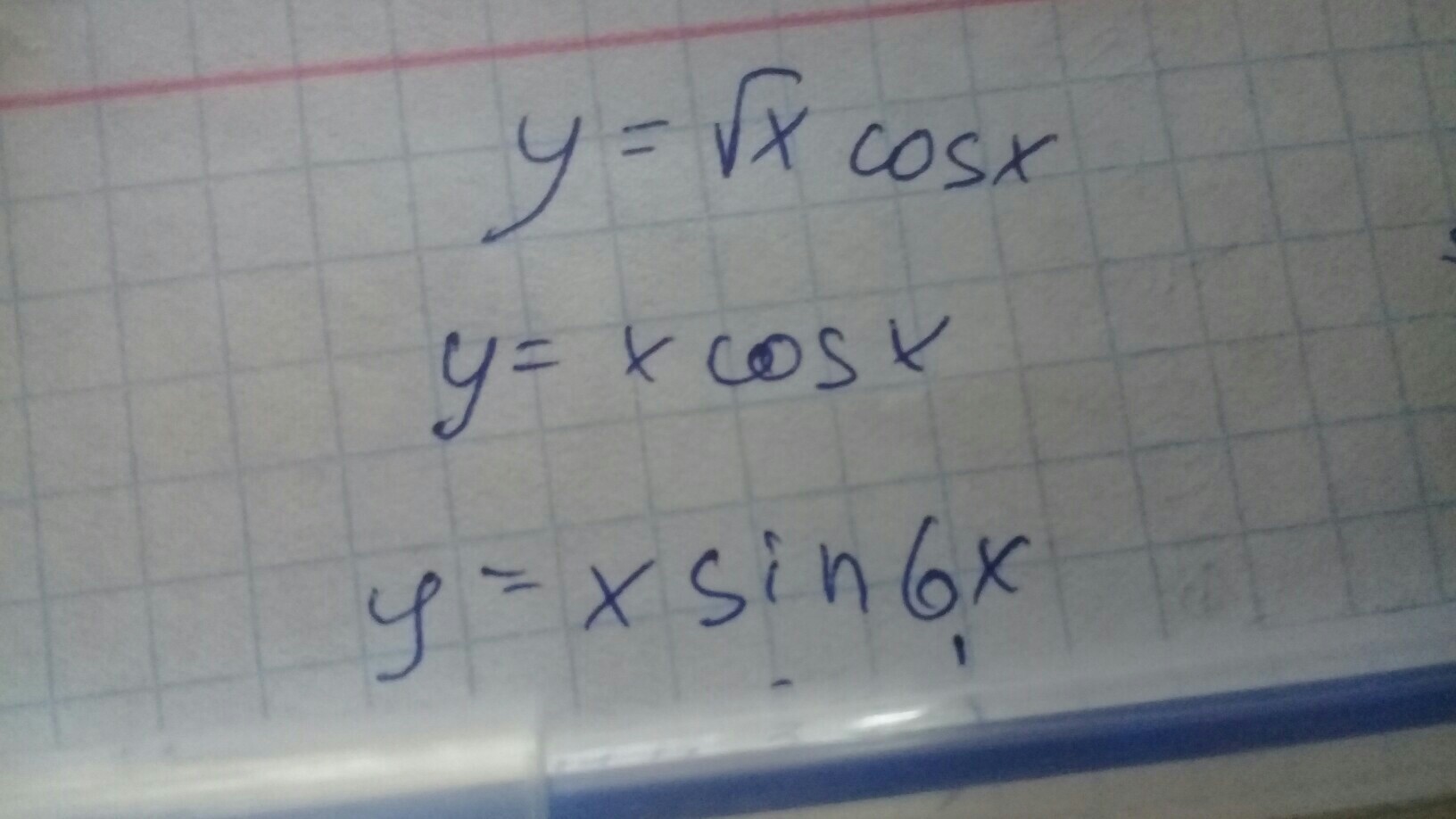Ответы
Ответ дал:
0
-------------------------------------------------------
Готово™
-------------------------------------------------------
Готово™
-------------------------------------------------------
Приложения:
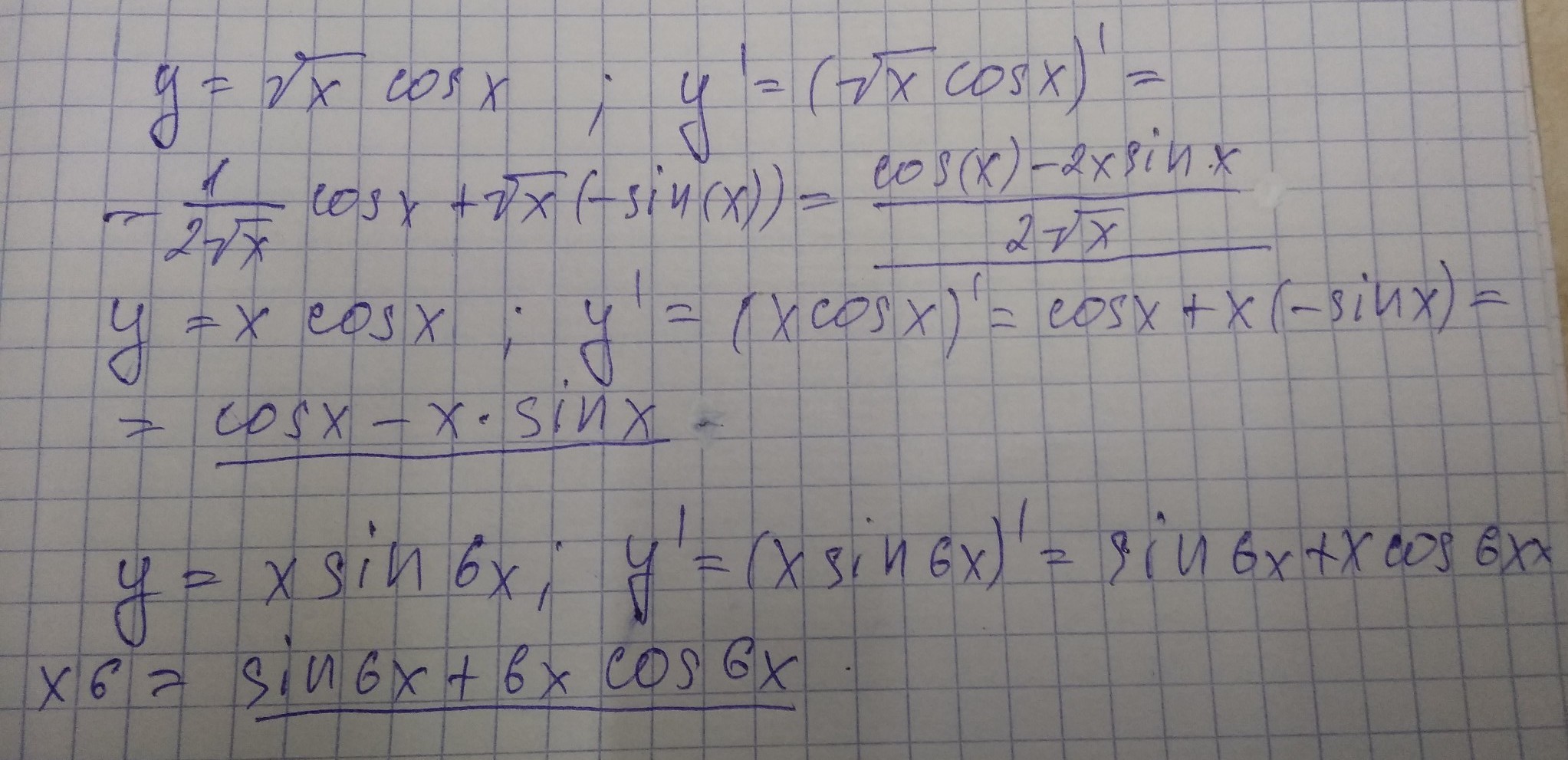
Ответ дал:
0
https://znanija.com/task/29362465 - помогите мне пожалуйста
Ответ дал:
0
Приложения:
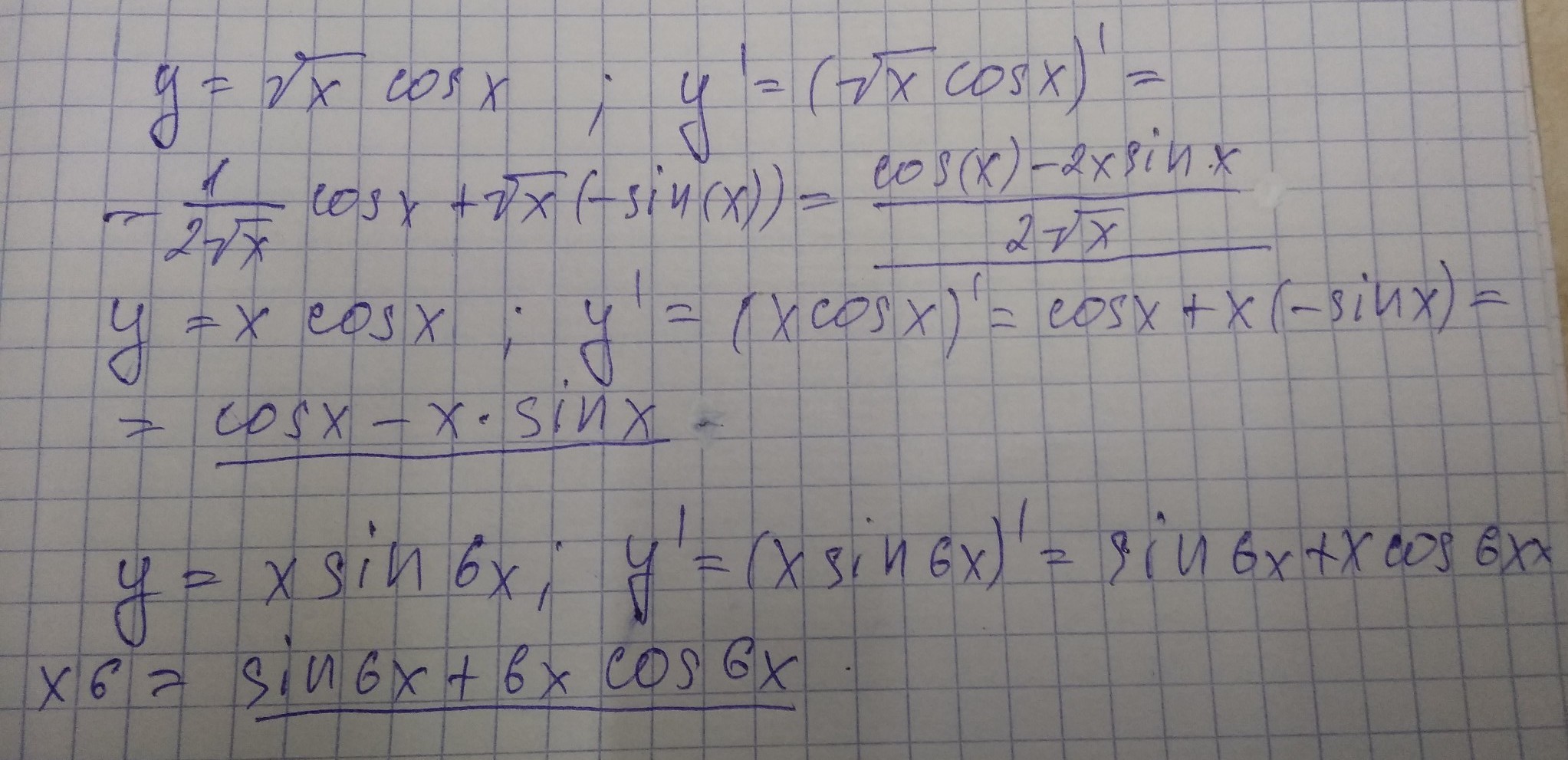
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад