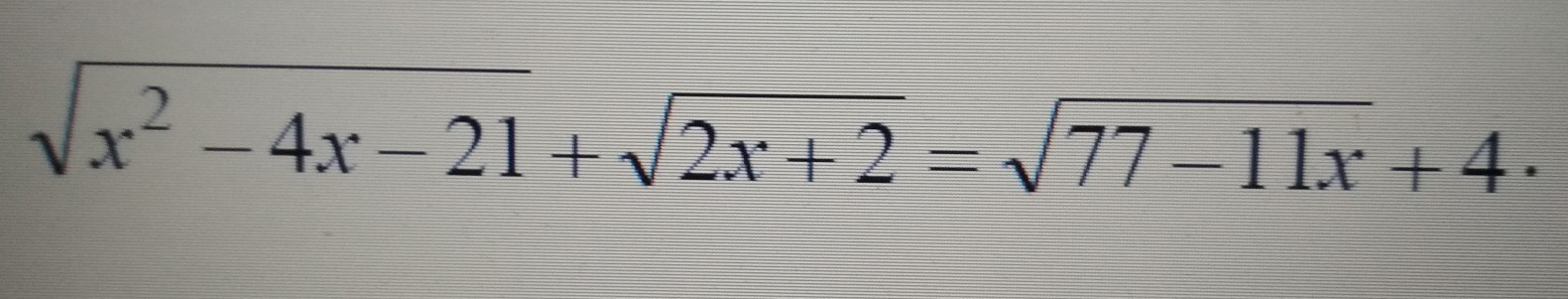Ответы
Ответ дал:
0
Запишем ОДЗ
Таким образом, x=7 - вся область допустимых значений. Проверим, является ли данное число корнем.
Ответ: 7
Ответ дал:
0
D(y):
1) x^2-4x-21≥0
По теореме Виета, равенства соблюдается при х={-3; 7}
(x-7)(x+3)≥0
х принадлежит (-бесконечность; -3] U [7; +бесконечность)
2) 2х+2≥0
х≥-1
3) 77-11х≥0
х≤7
х=7
при х=7:
√(49-4*7-21)+√(2*7+2)=√(77-11*7)+4
4=4
Ответ: {7}
1) x^2-4x-21≥0
По теореме Виета, равенства соблюдается при х={-3; 7}
(x-7)(x+3)≥0
х принадлежит (-бесконечность; -3] U [7; +бесконечность)
2) 2х+2≥0
х≥-1
3) 77-11х≥0
х≤7
х=7
при х=7:
√(49-4*7-21)+√(2*7+2)=√(77-11*7)+4
4=4
Ответ: {7}
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад