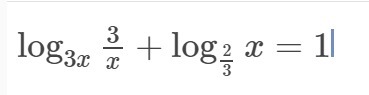Ответы
Ответ дал:
0
ОДЗ: (0;1/3) и (1/3;+∞)

Тут тупо переносим 1 и просто решаем, относительно t
Это просто(перенеси 1 налево и общий знаменатель), поэтому перейду сразу к t

Возвращаемся к замене:


Тут тупо переносим 1 и просто решаем, относительно t
Это просто(перенеси 1 налево и общий знаменатель), поэтому перейду сразу к t
Возвращаемся к замене:
Вас заинтересует
2 года назад
3 года назад
9 лет назад
10 лет назад
10 лет назад