Question

У трикутнику ABC медіана AM утворює із стороною AB кут 30 градусів. Знайти кут BAC якщо AB=2AC.

Answer 1

Розв'язок задачі у вкладенні

Answer 2

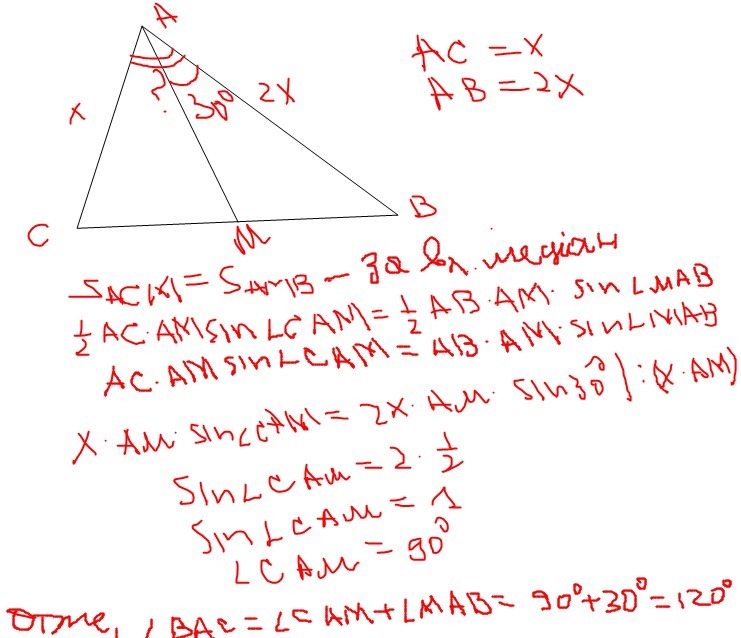
медиана делит треугольник на два равновеликих треугольника (у них площади равны): 0.5*АВ*АМ*sin(30°) = 0.5*AC*AM*sin(x)

2АC*(1/2) = AC*sin(x)

sin(x) = 1 ---> угол МАС = 90° ---> угол ВАС = 90°+30° = 120°

оказывается, очень мучиться не пришлось...

и второе решение даже изящное получилось))

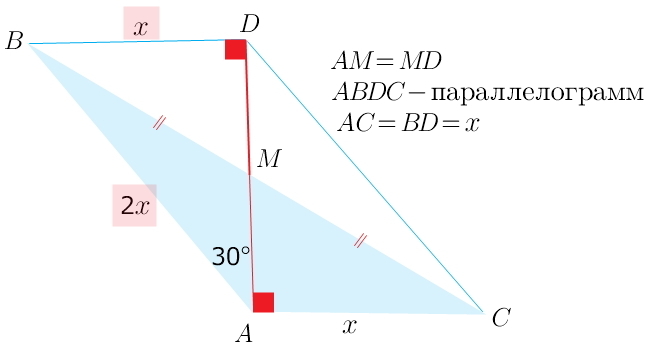
если продолжить медиану на ее же длину, то треугольник достроится до параллелограмма... в получившемся треугольнике ABD "легко" заметить, что сторона против угла в 30° равна половине другой стороны... это верно только для прямоугольного треугольника)) и ∠BDA=∠CAD как накрест лежащие при параллельных АС и BD и секущей AD...

Answer 3

Тоді так як писав раніше "Можна в даному трикутнику провести середню лінію і матимемо трикутник з кутом 30 градусів, сторони якого відрізнятимуться вдвічі і потрібно показати, що він прямокутний"

Answer 4

Дуже дякую всім!

Answer 5

Якщо нескладно поглянте будь ласка на добавлену мною ще одну задачу

Answer 6

Собственно говоря о вашем треугольнике. Ваш треугольник взять из правильного шестиугольника. Взяли просто и оторвали кусок правильного шестиугольника. И если достроить несколько элементов данного треугольника, то вы легко получите ваш тупой угол в 120°

Answer 7

Також можна і через середню лінію розв'язати