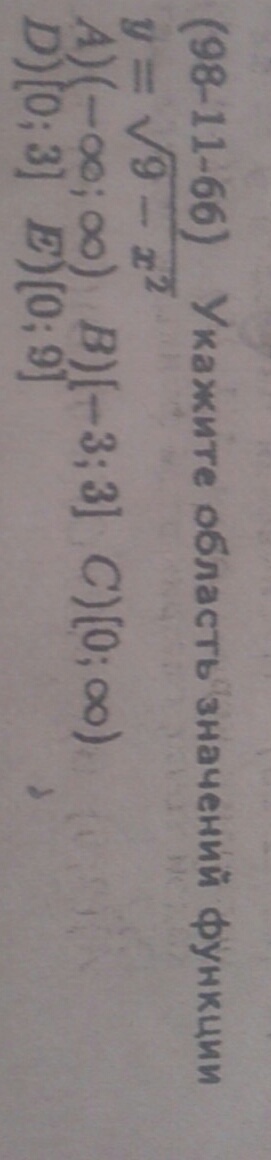Question

Помогите пожалуйста! Заранее благодарю!

Answer 1

Если приглядеться, можно заметить, что это уравнение полуокружности.
Возведем в квадрат обе части, получаем:
y² = 9 - x² ⇔ x² + y² = 3²
окружность радиусом 3.
Так, как исходная функция не принимает отрицательных значений, то область значений будет [0 ; 3]

Ответ: [0; 3]

Можно, конечно, немножечко по-другому. Область значений функции является областью определения обратной функции.

y = √(9 - x²)
Сразу отметим, что y ≥ 0
Теперь возводим в квадрат и выражаем x через y
y = 9 - x²
x² = 9 - y²
x = ± √(9 - y²)
Находим область определения
y∈[ -3 ; 3]
И т.к. функция не принимает отриц. значений, то
y ∈ [ 0 ; 3 ]

Answer 2

а как смотреть максимум и минимум?)

Answer 3

у функции 9-x^2 на отрезке -3 3 ? Или производная или свойства квадратной функции что минимум в вершине

Answer 4

А максимум только через производную находится?)

Answer 5

я же написал - по свойству квадратичной функции

Answer 6

спасибо))