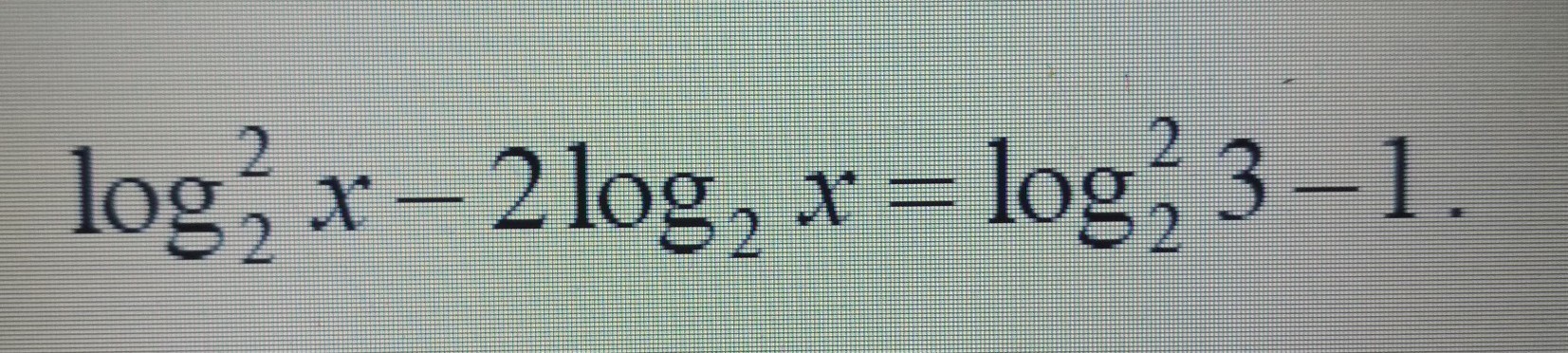Question

Найти произведение корней

Answer 1

$log_{2}(x) = y$
${y}^{2} - 2y - ( log_{2}(3) )^{2} + 1 = 0$

по т Виетта:
$y1 times y2 = 1 - ( log_{2}(3) )^{2}$
$y1 times y2= \ = 1 - ( log_{2}(3) )^{2} = \ = (1 - log_{2}(3))(1 + log_{2}(3))$

с другой стороны
по т Виетта:
y1+y2=2

нетрудно видеть, что

$y1 = 1 - log_{2}(3) = \ = log_{2}(2 ) - log_{2}(3) = \ = log_{2}( frac{2}{3} )$
$y2 = 1 + log_{2}(3) = \ = log_{2}(2 ) + log_{2}(3) = \ = log_{2}( {2} times {3} ) = log_{2}(6)$

возвращаемся к замене
$y = log_{2}(x)$
тогда

$log_{2}(x1) = log_{2}( frac{2}{3} )$
$log_{2}( x2 ) = log_{2}( 6)$

откуда x1=2/3 x2=6

x1*x2=(2/3)*6=4

Answer 2

Вы начали с теоремы Виета, а потом зачем то решали уравнение. log2(x)=y, пусть y1 и y2 корни уравнения, то по теореме Виета y1+y2=2 log2(x1)+log2(x2)=2 log2(x1*x2)=2 x1*x2=2^2=4. У Вас это как бы есть, но вы почему-то это не использовали.

Answer 3

Согласен. Спасибо за замечание.