Question

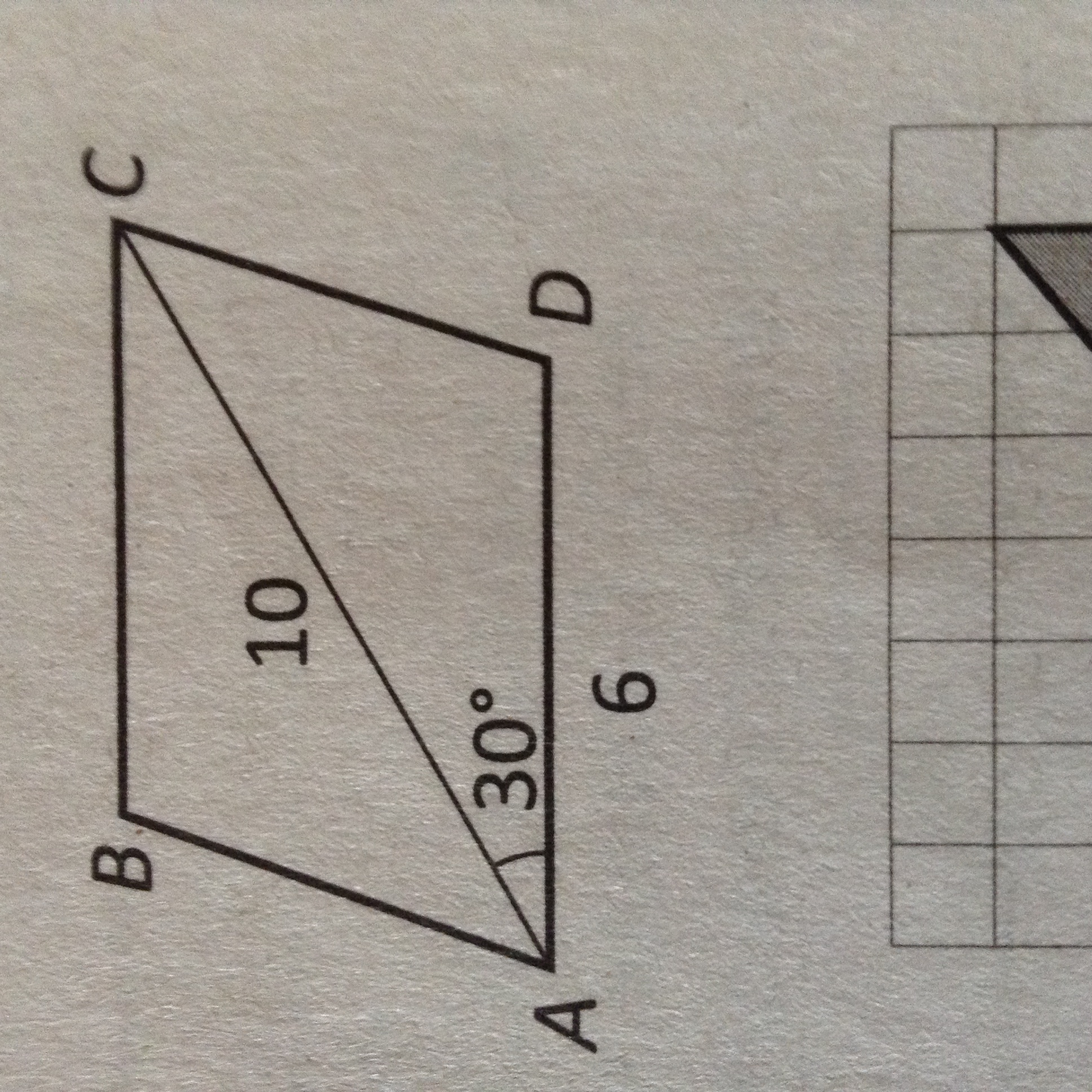
.Диагональ AC параллелограмма ABCD образует со стороной AD угол, равный 30 градусов. Найдите площадь параллелограмма ABCD, если известно, что AC = 10, AD = 6

Answer 1

Известно, что диагональ параллелограмма делит его на два равных треугольника. Найдем площадь параллелограмма через площадь треугольника АСД. S(АСД)=12 * АС * АД * sin30 = 12 * 60 * 12 = 15 (кв. ед)

S(АВСД) = 15 * 2 = 30 (кв. ед.)

Ответ: 30.

Answer 2

то что диагональ параллелограмма делит его на два равных треугоника неизвестно

Answer 3

если это Вам почему-то неизвестно, посмотрите соответствующую теорему

Answer 4

ой извините

Answer 5

Данная теорема очень просто доказывается. Противолежащие стороны параллелограмма равны, а диагональ - общая у треугольников. Отсюда равенство по трем сторонам.