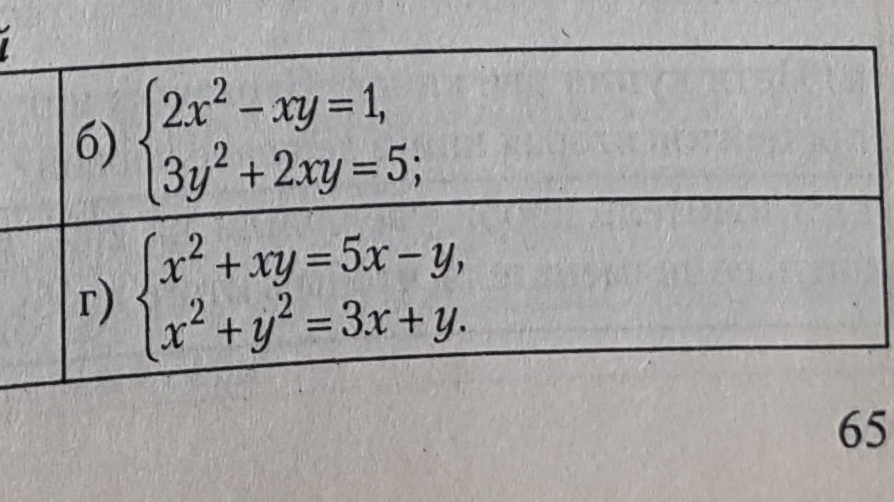Ответы
Ответ дал:
0
б)
Умножим обе части на
- 1-ая пара:
- 2-ая пара:
- 3-ая пара:
- 4-ая пара:
Ответ:
Пункт г) решается аналогично
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад