Question

а) Решите уравнение:
$dfrac{sqrt{sin x+0,5}cdot(0,5cdot log_{sqrt{7}}sin x +3cdot log_{343}cos x+dfrac{log_52}{log_57}) }{cos^26x-1}=0$
б) Укажите все корни этого уравнения из промежутка $( lg(cos 2pi); e^{2lnsqrt{2pi}} ]$

Answer 1

.......................

Answer 2

а) $sinx=-0.5$ или $log_{7}sinx+log_{7}cosx+log_{7}2=0$

Из 2-го уравнения следуют ограничения: $sinx>0; cosx>0$

1-й корень отпадает, остаётся только:

$log_{7}(2sinxcosx)=0$

$2sinxcosx=1$

$sin2x=1$

$x=frac{pi}{4}+2pi k$, k - целое

б) $lg(cos2pi )=lg1=0$

$e^{2lnsqrt{2pi}}=(e^{lnsqrt{2pi})^2=2pi$

То есть промежуток $(0; 2pi ]$

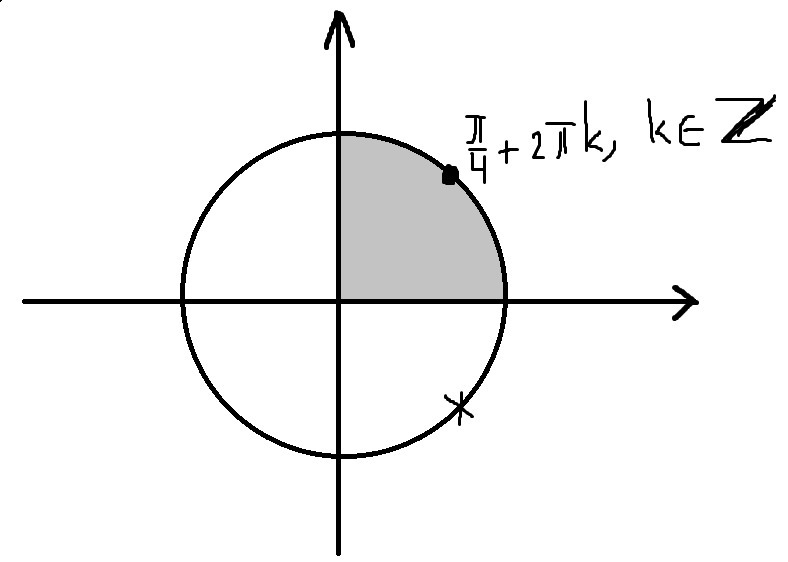
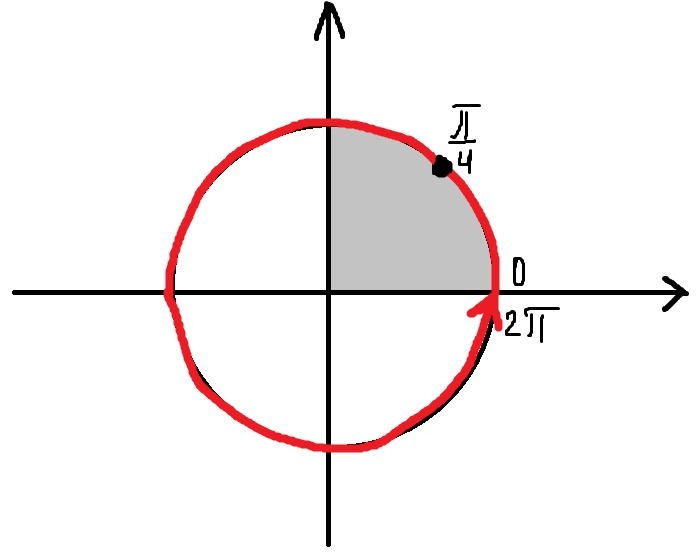
Отбор корней проведём с помощью тригонометрической окружности

Ответ: а) $frac{pi}{4}+2pi k,$ k - целое; б) $frac{pi}{4}$

p.s. написал, потому что ничего не понял в прошлом решении