Биссектрисы тупых углов при основании равносторонней трапеции делят ее большую основу на три равные часть и не пересекаются. Найдите отношение средней линии трапеции к ее меньшего основания, если градусные меры углов при основании равны 120 градусов
Ответы
Ответ дал:
0
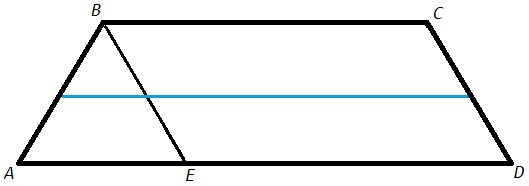
ABCD - трапеция, AB=CD, ∠ABC=120°, BE - биссектриса, AE= 1/3 AD
∠BCD=∠ABC=120° (углы при основании равнобедренной трапеции)
∠EBC=120°/2=60° (BE - биссектриса)
BE||CD (сумма внутренних односторонних углов 180°)
AD||BC (основания трапеции)
EBCD - параллелограмм (противоположные стороны параллельны)
BC=ED =AD-AE =2/3 AD
Средняя линия трапеции равна полусумме оснований.
(AD+BC)/2 =(AD +2/3 AD)/2 =5/6 AD
5/6 AD : 2/3 AD = 5/4
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад