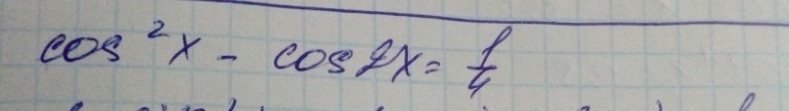Question

Помогите решить , пожалуйста

(cos^2)x-cos2x=1/4

Answer 1

$cos ^{2} (x) - cos(2x) = frac{1}{4} \ cos ^{2} (x) - cos ^{2} (x) + sin ^{2} (x) = frac{1}{4} \ sin {}^{2} (x) = frac{1}{4} \ sin(x) = frac{1}{2} : : : and : : : : : sin(x) = - frac{1}{2} \ x = frac{pi}{6} + 2pi : k : : : : : : : : : : : x = - frac{pi}{6} + 2pi : k \ x = frac{5pi}{6} + 2pi : k : : : : : : : : : x = frac{7pi}{6} + 2pi : k$
Если объединить решения , то получится :
$x = frac{pi}{6} + pi : k \ x = frac{5pi}{6} + pi : k$

Answer 2

Большое спасибо

Answer 3

К сожалению, вы неправильно решаете тригонометрические уравнения...

Answer 4

Всего лишь ошибка в периоде. Может быть, даже опечатка.