Question

В трапеции ABCD (AD || BC) диагонали АC и ВD перпендикулярны друг другу, AС = 5, BD = 13. Найти расстояние между серединами оснований.

Answer 1

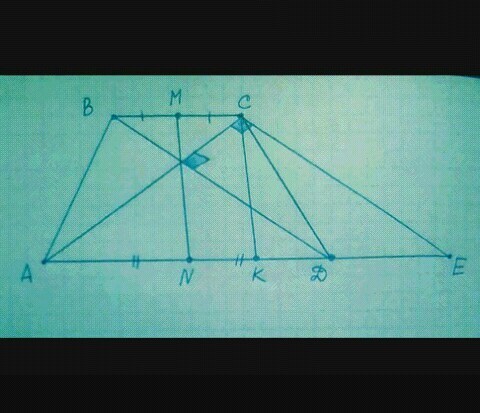
1) Осуществим дополнительное построение:
Проведём отрезок СЕ параллельно диагонали ВD => AC перпендикулярен СЕ.
Также проведём отрезок СК параллельно отрезку МN

Из этого следует, что четырёхугольник ВСЕD - параллелограмм ( СЕ || ВD , BC || DE ).
Aналогично, четырёхугольник МСКN - параллелограмм ( CK || MN, МС || KN )
Поэтому, BC = DE , MC = NK, BD = CE = 13
AE = AD + DE = AD + BC
AK = AN + NK = (1/2) × AD + (1/2) × BC = (1/2) × ( ВС + AD )
Значит, K - середина отрезка АЕ , АК = КЕ
Поэтому , МN = CK - медиана в ∆ АСЕ

2) Рассмотрим ∆ АСЕ ( угол АСЕ = 90° ):
" В прямоугольном треугольнике медиана равна половине гипотенузы " →
По теореме Пифагора:
AE² = 13² + 5² = 169 + 25 = 194
AE = √194

Значит, искомый отрезок MN, равный отрезку СК, имеет длину:
СК = MN = (1/2) × AE = (1/2) × √194 = √194/2


ОТВЕТ: √194/2

Answer 2

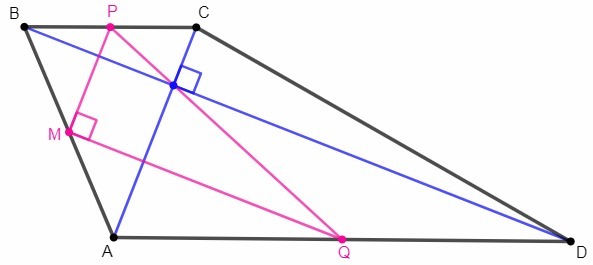
M - середина AB, P - середина BC, Q - середина AD

Средняя линия треугольника соединяет середины двух сторон, параллельна третьей стороне и равна её половине.

MP - средняя линия в ABC, MP||AC, MP=AC/2

MQ - средняя линия в ABD, MQ||BD, MQ=AD/2

AC⊥BD => MP⊥MQ

По теореме Пифагора

PQ=√(MP^2+MQ^2) =√(AC^2+AD^2)/2 =√194/2

Answer 3

Дополнительно. N - середина CD. MPNQ - параллелограмм Вариньона (середины сторон четырёхугольника являются вершинами параллелограмма). Так как стороны параллелограмма Вариньона параллельны диагоналям, а диагонали в данном случае перпендикулярны, MPNQ - прямоугольник. Диагонали прямоугольника равны, PQ=MN. То есть, если диагонали трапеции перпендикулярны, то отрезок, соединяющий середины оснований, равен средней линии.

Answer 4

Ошибочка: вместо AD должно быть BD.

Answer 5

MP - средняя линия в ABC, MP||AC, MP=AC/2
MQ - средняя линия в BAD, MQ||BD, MQ=BD/2
AC⊥BD => MP⊥MQ
PQ=√(MP^2+MQ^2) =√(AC^2+BD^2)/2 =√194/2

Answer 6

Ты же сам сказал половине. Почему AC и BD у тебя полностью?

Answer 7

√((AC/2)^2 +(BD/2)^2) =
√(AC^2/4 +BD^2/4) =
√((AC^2 +BD^2)/4) =
√(AC^2 +BD^2)/2