Question

x^2-9>0 (ответ -бесконечность ,-3) но не мпогу понять почему , объясните

Answer 1

Напишу решение несколькими способами

1) Метод интервалов

x²-9>0

(x-3)(x+3)>0

___+___(-3)___-___(3)___+___

x∈(-∞; -3)U(3; +∞)

2) Разбитие на совокупность систем

x²-9>0

(x-3)(x+3)>0

Имеем произведение двух чисел, которое должно быть больше нуля. Так как "+" на "+" дает "+" и "-" на "-" дает "+"

$(x-3)(x+3)>0 Leftrightarrow left[begin{array}{I} left{begin{array}{I} x-3>0 \ x+3>0 end{array}} \ left{begin{array}{I} x-3<0 \ x+3<0 end{array}} end{array}} Leftrightarrow left[begin{array}{I}left{begin{array}{I} x>3 \ x>-3 end{array}} \ left{begin{array}{I} x<3 \ x<-3 end{array}} end{array}} Leftrightarrow left[begin{array}{I} x>3 \ x<-3 end{array}}$

x∈(-∞; -3)U(3; +∞)

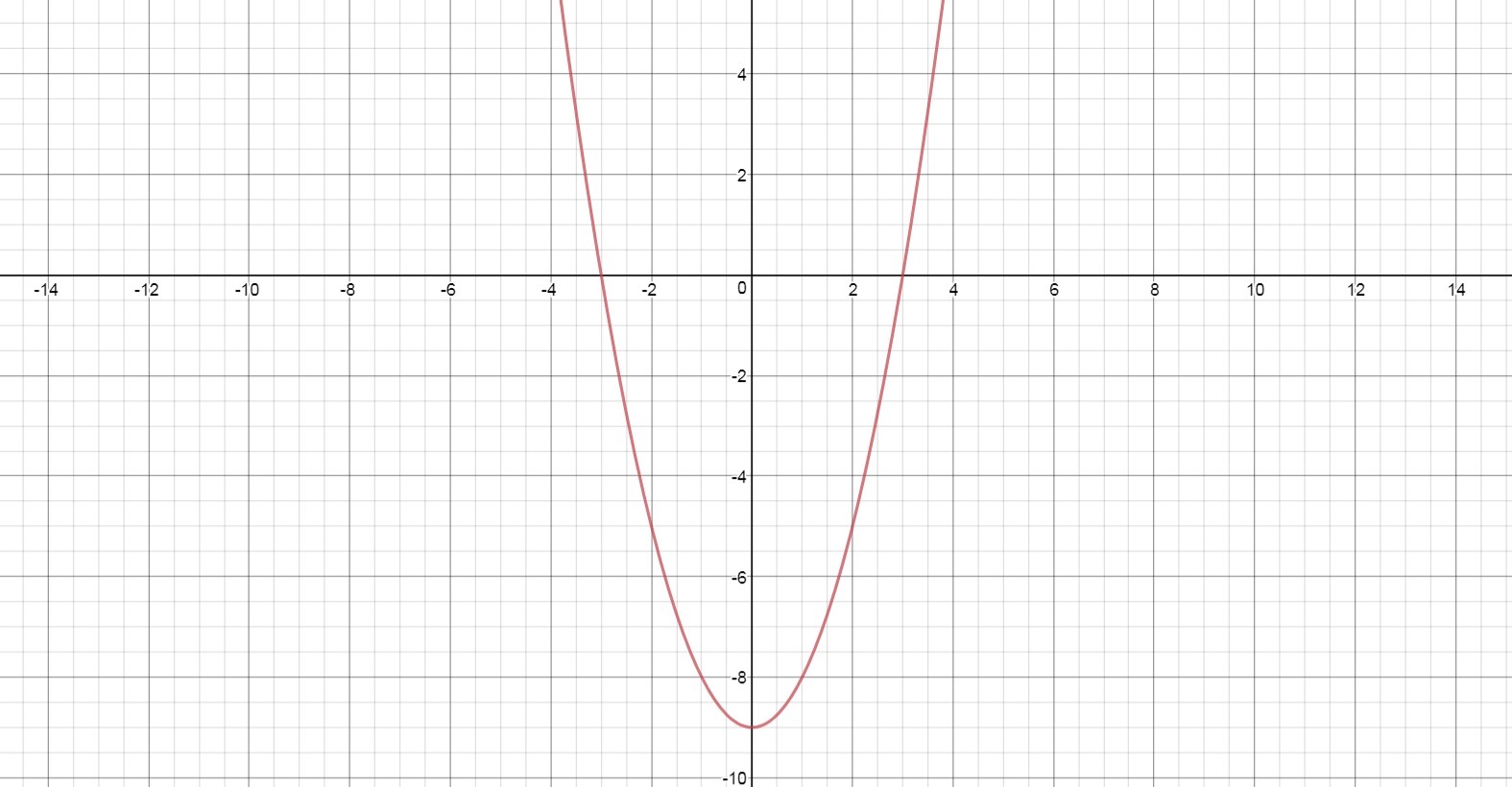
3) Графическое решение. Самое наглядное.

Строится парабола y=x²-9, после чего выбираются интервалы, где функция принимает значения больше нуля. График прикреплен.

x∈(-∞; -3)U(3; +∞)